Reference no: EM131035238

Question 1 - Antel Corp., is a large manufacturer of a broad range of computer chips with a market value of capital (Equity + Net Debt) of $200 billion. It is considering the introduction of a new line of chips for handheld devices in 2013. Antel's revenues from the new line are projected to be $3 billion per year between 2013 and 2015 (3 years), after which the chip will become obsolete. The R&D expenses per year during the four years of development (2008 to 2011) were $0.5 billion, and the only capital expenditures required to set up the production line are $1 billion, to be paid at the end of 2012. Capital expenditures in the new line can be depreciated using the 5 year straight-line method, and the salvage value of the fixed assets is expected to be zero after they are fully depreciated. Both, the current working assets (the sum of necessary cash, accounts receivable, inventory, etc.) and the automatic sources (the sum of accounts payable and accrued expenses), required to operate and distribute the new line are expected to be $0.85 billion and to increase at a 17.5% per year. The line should yield operating profit margins of 20% (Note: operating profit margin = 100 x EBIT/Sales).

a) Suppose that Antel uses a weighted average cost of capital of 10% as a benchmark for its new chip projects. Calculate the NPV of the new project line (the corporate tax rate is 40%).

Antel hires you to assess whether 10% is the right discount factor to evaluate the new chip line. Antel has an equity beta of 0.9 and .a market equity to capital ratio of 1.2. The risk free rate is 3%, the market risk premium is 6%. Assume that Antel is currently at its target capital structure and it invests any excess cash in risk free assets.

b) What is the WACC of Antel?

c) Specialised manufacturers of handheld device chips have average asset betas of 1.0. Would the WACC using this asset beta be higher or lower than Antel's WACC? Which WACC would you recommend Antel to use in the valuation of the new project? Explain.

Antel's CFO is in the process of re-evaluating the firm's capital structure and hires you to provide expert advice.

d) Your research indicates that if Antel changes to a debt to capital ratio of 0.1 (at market values), the cost of debt will be 5%. Calculate the present value of the tax related incremental cash flows in 2013 if Antel switches to the new capital structure by the end of 2012.

e) Given your answer in part d), can Antel's market equity to capital ratio of 1.2 be the optimal capital structure? Why or why not?

 Question 2 - Firm B intends to bid for firm T in a hostile merger. Before the announcement of the merger negotiations, the biding firm (firm B) had 100 million shares trading at $2 per share while the target firm (firm T) had 5 million shares trading at $5 each. Firm B believes that, after acquiring control of firm T, it can implement managerial changes that will generate a stream of cash flows of $0.5 million after one year, and will grow at a 2% rate forever. An adequate risk-adjusted discount rate for these synergies is 7%.

Firm T is owned by dispersed shareholders. For this reason firm B is planning to implement a two-tier offer. The terms of the unconditional two-tier offer are set by the management of firm B as follows: the first 60% of the shares of T tendered will be bought at a price of $7 in cash, and the second 40% will receive 2.5 new shares of B per share of T. (Note: if 100% of shareholders tender, then each tendered share receives the first tier bid with 60% probability and the second tier bid with 40% probability).

The bidding firm has currently no toehold on the target firm. There are no transaction costs associated with this deal. The offer is unconditional and shareholders believe that it will succeed.

a) Carefully describe what is the free-rider problem in conditional tender offers when shareholders are dispersed. Explain how two-tiered offers can help to solve this problem.

b) Calculate the stand alone value of both firms (B) and (T) and the synergies. Compute the number of shares and the share price of the new combined firm if the two-tiered offer is accepted (note: remember that the first-tier cash exits the firm). Calculate the value that the second tier sellers get. Is this two-tiered offer likely to work? Why?

From now on, assume that firm B can be in a good or a bad state. In a good state its shares will soon be worth $3, while in a bad state its shares will soon be worth $1. The management of firm B knows perfectly which state the firm is in, but this is private information to them only. The current price of $2 per share reflects the market expectation over these two states. The synergies between A and B are as in the previous sections and they are independent of the state of the firm.

c) Calculate the profit of the proposed two-tier offer for a good and a bad firm. Show that by making the offer, the firm reveals whether it is in a good or a bad state.

d) Using the result in c) calculate again the value that the second tier sellers get. How should the market react to the announcement of the two tiered offer?

e) Suppose that firm B could pay the second tier with debt of the new merged firm instead of with shares. Intuitively explain how would that affect the selection issues in part c). (Note: you do not need to perform any calculations in this part, but clearly explain what are the forces at work).

Question 3 - Consider a world in which the assumptions of the Modigliani and Miller theorem hold. There are two twin firms, A and B that are identical in their economic activity. Both of them will have exactly the same unique and positive risky cash flow at the end of the year (X). Then they will dissolve. Currently firm A has 10m shares trading at £12 each and no debt. Firm B has 10m shares trading at £8 each. Firm B also has debt that matures in one year. The promised debt repayment of firm B is £22m and the current total market value of firm B's debt is £20m. As a trader in an investment bank, you are free to trade (including short sales) as much as you want in these securities. However you have two restrictions. i) Your risk officer does not allow you to hold more than £5m in the equity of any firm. ii) The net amount of funds that you invest at the end of the day has to be zero (i.e. in order to buy something, you need to sell something of equal value). Assume, for now, that your trading activity does not change the price of the securities.

a) Construct your optimal trading strategy to take maximum advantage of this situation.

b) How much risk are you taking with this strategy? How would you try to convince your risk officer to release you from restriction i)?

c) Now relax the assumption about your trading activity not affecting the price of the securities. What is the likely impact of your trading? Briefly explain the main advantage of valuation conditions that are based on arbitrage opportunities rather than equilibrium predictions?

d) Suppose that, before arbitrage occurs, firm A's equity is correctly valued at £12 per share, and its beta is 5/3. Suppose that firm B's debt is risk free and also correctly priced at £20m. What is the cost of equity of firm B? (Note: the market risk premium is 6%)

e) Suppose that the conditions in d) hold, that is, the equity of firm B is undervalued before arbitrage occurs. Suppose an individual investor wants to take advantage of the arbitrage opportunity, but she can only buy or sell stock and deposit cash in the bank at the risk free rate. What is the systematic risk (beta) of her investment if she buys firm B's stock? What investment strategy would allow a risk averse investor to buy B's stock but expose her to the same systematic risk of buying A's stock?

Question 4 - Consider observing the following bonds:

Bond	Coupon rate (%)	Maturity	YTM (%)
A	0	1 year	5.10
B	6	2 years	5.60
C	7	3 years	7

Coupon payments are annual, face value is $100, and bid-ask spreads are zero.

1. What are the prices of the above bonds?

2. What are the spot rates for year 1, year 2, and year 3?

3. Suppose you also observe bond D with two years to maturity, 12% coupon, priced at $115. Is it possible to construct an arbitrage, given the bond prices? If so, what is the trading strategy that produces the arbitrage?

4. What is the Macaulay duration of bond C?

5. Suppose for the rest of this question that the term structure is flat at 6%. Suppose also that one year from today the term structure will be flat at either 5% or 7%, with equal probability. Compute a non-putable two-year zero bond price today. (Hint: When bond is putable, the bond holder has a right to sell back the bond to the issuer at a pre-specified strike price besides the right to the cash-flow of the bond.) Compute the price of the two-year zero-coupon bond in one year under both scenarios for the term structure.

6. Suppose the buyer of the bond has a right to sell it back at 94.5. That is, the bond is putable. Under which scenario of the flat term structure: at 5% or 7%, would the buyer exercise the right to sell back the bond in one year?

7. What is the price of the two-year zero-coupon putable bond today?

 Question 5 - Consider two portfolios A and B in a CAPM economy. The expected return of portfolio A is E(R_A) = 15% and the expected return of portfolio B is E(R_B) = 3%. The CAPM beta for portfolio A is β_A = 1.2 and for portfolio B is β_B = 0. The standard deviation of the market portfolio is 20%.

1. Suppose A and B are correctly priced according to the CAPM. Derive and plot the security market line and label the intercept and market risk premium.

2. Suppose there is a well-diversified portfolio C where β_C = 2 and E(R_c) = 20%. Is there an arbitrage opportunity? If yes, construct one such strategy and show its cash-flows and risk.

3. Suppose portfolio C is not well diversified and the standard deviation of portfolio C's idiosyncratic risk is 30%. What is the total variance of portfolio C? Is the arbitrage strategy you constructed in part ?? still an arbitrage strategy?

4. What is the tangency portfolio in the general CAPM economy? Derive the CAPM equation and state the assumptions.

5. If the CAPM is valid, consider the stock of company D where OD = 0.9. Company D is paying a dividend of $3 one year from now. This dividend is expected to grow at 10% for the next three years (from year 1 to year 2, from year 2 to year 3, and from year 3 to year 4) and at 3% forever after (that is, from year 4 on). The payout ratio is 80%. Determine its stock price and its PVGO.

6. Which of the following observations would provide evidence against the semi-strong form of the efficient market hypothesis and why?

a. In any year some mutual funds outperform the market.

b. Following an earning's announcement, one can form trading strategies to make abnormal returns.

7. Which of the following observations would provide evidence against the weak form of the efficient market hypothesis and why? j2 marks]

a. A company insider makes abnormal returns by trading the company stock.

b. Technical analyses generate abnormal returns.

Question 6:

 1. Fill in the missing numbers in this table of stock index futures prices.

Country	Index Name	Index Value	Dividend Yield (annualized)	Spot interest rate (annualized)	Futures Maturity (months)	Futures Price (same unit as index value)
UK	FTSE100	6460.73	1.10 %	2.30 %	6	???
Netherlands	AEX	509.22	???	4.05 %	9	520.25

2. It is now January. The current yield curve is flat at 5%. The June futures price for gold is $346.30, whereas the December futures price is $360.00. Assume the net convenient yield is zero. Is there an arbitrage opportunity here? How would you exploit it? Show the cash-flows.

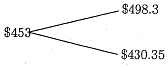
3. The current price of Google common shares is S₀ = $453. In this problem, we will price an at-the-money European straddle on Google with a maturity of three months. Note that the strike price is given. A straddle consists of a long position in a call option and a long position in a put option on Google stock with the same strike price. Assume that Google will not pay dividends in the next three months, and that the yield curve is flat at the annual rate of 5% (assuming continuous compounding).

Suppose that over the next three months Google will either go up by 10% or down by 5%. That is, the stock price of Google moves according to the following tree

In this part of the problem, we will calculate the value of the straddle directly, i.e., without considering the call and the put separately.

a. Draw the pay-off tree for the at-the-money European straddle on Google.

b. Find the replicating portfolio for a three-month at-the-money European straddle on Google. Calculate the price of this option using the replicating portfolio method.

c. What are the risk-neutral probabilities of the up and down moves of Google? Calculate the price of the straddle using the risk-neutral probabilities.            

4. Given your success in pricing the three-month straddle, your boss asks you to price the six-month straddle on Google. You assume that the interest rate will not change, but the Google stock can go up by an additional 10% or it can go down by an additional 5% in the second three-Month period regardless of what has happened in the first three months.

Find the price of the at-the-money six-month European straddle on Google.

a. Draw the binomial tree for the possible prices of the Google stock in the future.

b. Find the final pay-offs of the straddle and, using the method of risk-neutral probabilities, find the straddle price for each node of the binomial tree including the node at time zero.