Calculate the moments in the strips using elastic analysis

Reference no: EM133112755

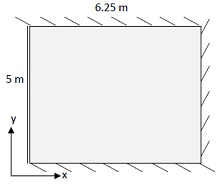
Question: A 150 mm thick reinforced concrete slab is supported on all 4 sides as denoted in the diagram.

• The design moment capacities are

ΦM_ux⁺	10 kNm/m
ΦM_ux^-	12 kNm/m
ΦM_ux⁺	15 kNm/m
ΦM_ux^-	18 kNm/m

1879_Reinforced concrete slab.jpg

• All reinforcing is Grade N.
• Permanent load (DL) and imposed load (LL) factors are as given in Lecture 1.
• In addition to the self-weight there is a nominal permanent load of 1 kPa for permanent partitions.
• Reinforced concrete nominal density is as given in Lecture 1.

Show all working (including differentiation for the yield-line method).

Question 1: If the slab is supported on all 4 sides as denoted in the diagram, use published coefficients that apply only to ductile rectangular slabs with standard support conditions and uniform loading in AS 3600 to calculate the nominal value of uniformly distributed imposed load (LL) that the slab can support.

Question 2: If the slab is supported on 4 sides as denoted in the diagram, use yield-line theory to calculate the nominal value of uniformly distributed imposed load (LL) that the slab can support. [Additional information: The distance in the x direction from the left edge (the simply supported edge) to an intersection point of yield-lines is 1.747 m].

Question 3: If the slab is supported on 4 sides as denoted in the diagram, use the strip method to calculate the nominal value of uniformly distributed imposed load (LL) that the slab can support. For the strip method distribute the total load 30% spanning in the long direction and 70% spanning in the short direction, and calculate the moments in the strips using elastic analysis.

Question 4: If the slab is simply supported on 4 sides (instead of supported as denoted in the diagram), use yield-line theory to calculate the nominal value of uniformly distributed imposed load (LL) that the slab can support.

Question 5: In 100 words or less, explain why the 4 values for the nominal value of uniformly distributed imposed load (LL) that the slab can support are different.

Reference no: EM133112755

Questions Cloud

Calculate the capital element of each payment : A $350,000 non-registered annuity provides a monthly payment of $1,500 over 20 years. Calculate the capital element of each payment.

Applied an annual exclusion to the transfer : Assume Mary made a gift of property in 2019 with a fair market value of $100,000 and an adjusted basis of $40,000 to Dominic. What would Dominic's basis in the

Service about rejecting an irregular check : Create a script in which there will be an bank employee and the rest will be as bank customers.

Estimate of the asset beta for abc corp : Consider the following information regarding corporate bonds:

Calculate the moments in the strips using elastic analysis : Calculate the nominal value of uniformly distributed imposed load (LL) that the slab can support and calculate the moments in the strips using elastic analysis

Psychological foundations of leadership : You were introduced to the psychological foundations of leadership along with several different models of leadership.

Loan analysis case study question : 1) You are a Risk Manager for this bank. What risk measures and all the Qualitative and Quantitative Risk Analysis you will perform in the loan sanction

Recommend investing in tesla stock : Explain would you recommend investing in Tesla (TSLA) stock?

Estimate the cost of capital for ruivo : 1). Estimate the cost of capital for Ruivo. 2). Using DCF method, estimate the stand-alone value of equity in Ruivo.

User Account

All Pages