Reference no: EM13962441
QUESTION 1:
(a) (i) Show that
i=1Σn ei/n = (e1/n(1-e))/(1-e1/n).
Hint: The series i=1Σn ei/n is a geometric series. Use your knowledge of geometric series from high school to evaluate this series.
(ii) Use l'Hopital's rule to evaluate
limt→∞ [t(1 - e1/t)].
Hint: Recall the methods using l'Hopital's rule from Mathematics 1A where we had limits in the form "∞ x 0".
(iii) Recall the definition of the definite integral:
a∫b f (x) dx = limn→∞ i=1Σn f(xi*)Δx
where the notation is that which is used in Lecture 1. Use the definition to find the area between f (x) = ex and the x-axis between x = 0 and x = 1. You may require your results from parts (i) and (ii) above.
(b) The manager of the local "McMuckies" fast food outlet has found that the average waiting time that her customers have to wait for service is 3 minutes.
(i) Find the percentage of customers who have to wait more than 4 minutes.
(ii) Find the percentage of customers that are served within the first 2 minutes.
(iii) Sales have been falling, so the manager wants to advertise that anybody who isn't served within a certain number of minutes gets a free burger. But she doesn't want to give away free burgers to more than 3% of her customers. What should the advertisement say?
QUESTION 2:
Recall Torricelli's law for a liquid draining from a tank:
A(h) dh/dt = -k√h
where the notation is that used in Lecture 6.
(a) Show that, in general, the differential equation in Torricelli's law may be solved by separation of variables. State any assumptions you have used.
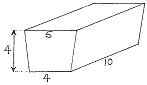
(b) (i) A dairy farmer has a large vat three-quarters filled with milk. The vat is in the shape of a trapezoidal prism with length 10 metres, perpendicular height 4 metres, lower width 4 metres and upper width 5 metres. See the diagram. The drain at the bottom of the tank is opened. Use Torricelli's law with k = 0.03 to determine the depth of the milk at any instant after the drain has been opened.
(ii) Use Wolfram Alpha to obtain a plot of h versus t.
(iii) Determine how long it will take the milk to completely drain from the vat.
(c) Is it possible to design a tank such that the depth of the liquid, h, will be a linear function of time, t ?
Provide assumptions and detailed calculations either proving the impossibility of such a tank or showing the dimensions of a tank for which this is possible.
Note that a group which is able to provide sound mathematical reasoning will gain more marks than a group using pure guesswork.
|
New and more effective antimicrobials are developed
: New and more effective antimicrobials are developed every year. Many of these are effective in treating common ailments as well as more serious infections. But what are more potential consequences with new antimicrobial development?
|
|
Compare and contrast the innate and the acquired immune
: Compare and contrast the innate and the acquired immune responses with respect to the time of onset, the immune activators, and the primary immune cell types that involved.2. Define immunogenicity and explain its relevance to bacterial infections, vi..
|
|
Producer of expensive-high-tech computer components
: Assume that you are the supply chain manager for a producer of expensive, high-tech computer components. Identify the most suitable method(s) of transporting your product in terms of cost, transit time, reliability, capability, accessibility, and tra..
|
|
What is the effect of this variable on the population size
: What is the effect of this variable on the population size estimate? On the number of "misses"? Are there any other interesting patters?Why might marked animals be easier to recapture?
|
|
Calculate the length of the proposed section of train track
: Determine how long it will take the milk to completely drain from the vat - Calculate the length of the proposed section of train track - Find the percentage of customers who have to wait more than 4 minutes.
|
|
What is the effect of this variable on the population size
: What is the effect of this variable on the population size estimate? On the number of misses? Are there any other interesting patterns?What can you do to minimize this bias in the real world? Can you solve the problem by increasing S1 and S2?
|
|
Ocean acidification on primary producers
: What is the Influence of ocean acidification on primary producers?
|
|
Define a perfectly hard boiled egg
: Define a perfectly hard boiled egg, what are some errors than can occure when you are bililing 12 eggs 3 in each pan and each pan boils for a different amount of time, and you are using differnet size pans and they are metal
|
|
Consulting firm that has continued to operate and grow
: We Guessed & You're Wrong is a consulting firm that has continued to operate and grow. In fact, business has increased to the point where new partners or staff might be considered. A new partner would bring capital of $1,000,000 to the firm and addit..
|