Reference no: EM133037599

Question 1: Driven beaded string. A string with N beads, each of mass m and spacing a, is under tension T. At the left, the string is attached to a fixed wall, as usual. However, on the right, it is attached to a wall which oscillates up and down with amplitude h and angular frequency ω_d.

This means that the "fictitious bead" on the left has y₀ ≡ 0 as usual, but the fictitious bead on the right has y_N+1≡ hcos ω_dt. The differential equations of motion for this system are the same as for the undriven case (because the way the beads interact with each other is unchanged); only the boundary conditions are different.

(a) Explain why it's reasonable to guess that a solution for this problem would be y_j = Y_j cos (ω_dt - δ).

(b) Given the form of the above guess, explain why we expect that Y_j need not equal y_J0.

(c) Since the differential equations of motion are the same as for the undriven case, it's reasonable to guess that the amplitudes Y vary with position in the same way, that is, it's reasonable to guess Y_j = A sin αx_j, where the values of A and α are to be determined. Use y_N+1  ≡cosω_dt to find δ and A in terms of α, h, a, and N.

(d) Plug our guesses y_j = cos (ω_dt - δ) and Y_j =^? A sin αx_j into the equation (7.1.2) (which 'was derived simply by applying F = mx¨ to mass j):

-T/ma (-y_j-1 + 2y_j - y_j+1) = y¨_j

Verify that the guesses work, and show that cos (α a) = 1 - ω²_d/(2T/ma)

(e) Explain why the above implies that if ω_d > 2√(T/ma) then α is complex. Hint: Set α = α_r + iα_i;, uxe cos (α a) = Re [e^{iα a}), and show that for ω_d > 2 √(T/ma), α_i must be nonzero.

(f) Explain why a complex value of α means that the wave damps exponentially in space. Hint.- recall that sin x = Im [e^ix].

(g) What does that phrase "damps exponentially in space" mean?

(h) Why is it reasonable that the frequency 2√T/ma should be the highest frequency which does not give exponential damping in space?

Question 2: A string of mass M and length L is attached to walls at either end, and is under tension T. The string is held at rest in the following shape: y = B for L/2 < x < 3L/4, and y = 0 for the rest of the string. The string is released at i = 0. (a) Find y(x, t}. You may express your answer as an infinite series, so long as you have defined all the symbols in your series. (b) Using (You may wish to complete

Question 3: A string of mass ñf and length L is attached to walls at either end, and is under tension T. At t = 0, the string has the following shape: y = B for L/2 < x < 3L/4, and y = 0 for the rest of the string. At t= 0 the velocity distribution is y E for L/4 < x  < L/2 and y 0 for the rest of the string. E has units of mls. Given these initial conditions, find y(x, t). (Note that this velocity pattern is not the same as the initial position pattern - one is nonzero on the right side of the string, and the other is nonzero on the left side of the string.) You may express your answer as an infinite series, so long as you have defined all the symbols in your series.

Question 4: A continuous string with mass per unit length μ is stretched with tension T between two walls, one at x = 0 and the other at x = L. At t = 0, its shape is given by y (x, t = 0) = L/100 x²/L², and it is at rest. What is the complex coefficient for the n = 2 mode in the normal mode expansion for these initial conditions? You may need the following integral (given in the form you would find it in an integral table):

∫x²sinaxdx = 2x/a²sinax + (2/a³ - x²/a) cos ax.

Question 5: A string of mass M and length L is attached to walls at either end, and is under tension T. Prior to t = 0, the string is held fixed with the following shape:

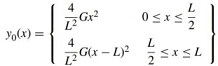
(a) Sketch this shape.

(b) At t = 0, the string is released. For the normal mode expansion, briefly explain why it is unnecessary to calculate the imaginary parts of the expansion coefficients.

(c) Calculate the coefficients in the normal mode expansion. lt might be helpful to note the solutions to the following integrals:

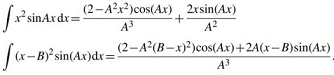
(d) You should have found that coefficients for the even n terms in the expansion are all zero. Explain why, based on symmetry.

(e) Write an expression for y(x, t). You may express your answer as an infinite series, so long as you have defined all the symbols in your series.