Reference no: EM132586539
Epidemiology Assignment -
1. All proportions are ratios, but not all ratios are proportions.
A. True
B. False
2. Which of the following are frequency measures?
A. Birth rate
B. Incidence
C. Mortality rate
D. Prevalence
E. All of the Above
F. None of the above
3. For each of the fractions below, indicate whether it is a ratio, a proportion, a rate, or none of the above
A. Ratio
B. Proportion
C. Rate
D. None of the above
___1. (# of women in the country who died from breast cancer in 2010)/(# of women in the country who died of heart disease in 2010)
___ 2. (# of people in State A who died from lung cancer in 2014 )/(estimated revenue ($)in State A for cigarette sales in 2014)
___ 3. (# of women in City A newly diagnosed with lung cancer in 2017)/(estimated # of women living in State A on July 1, 2017)
___ 4. (# of men who reported having heart disease in 2016 in a national survey )/(# of person-years contributed through 2016 by men intitally enrolled in the survey )
____5. (# of children in State A who were injured in 2018 )/(# of children in State A in the same period)
4. Using Behavior Risk Factor Surveillance System (BRFSS) evaluate the following:
A. What is the overall percentage of persons in the State of Massachusetts who use e-cigarettes in 2016?
B. Using the Confidence Intervals, compare and contrast that total with the crude prevalence obtained in 2017.
C. Which age group shows the highest use of e-cigarettes in Massachusetts in the year 2016?
D. How do the total percentages of e-cigarette use in Massachusetts for the years 2016 and 2017 compare to the state of Colorado over the same two years?
E. For the State of Colorado, which age group and gender have the highest crude prevalence for the year 2016?
F. Given your comparisons, is there any trend that you see occurring between e-cigarette use by state, age, and/or gender?
5. The incidence of a chronic disease in a population may be decreased by:
A. Prolonging the lives of persons with the disease
B. Decreasing the case-fatality rate for the disease
C. Improving the treatment of the disease once it has been diagnosed
D. Primary prevention
E. Secondary prevention
Applied Problem Solving
6. An infectious disease is introduced into a school with 1200 students. Fortunately, the disease only lasts a few days, and all of the infected students recover and then have long lasting immunity against the disease (they can only be infected once). The incidence rate for the outbreak, which begins the first week of school, remains constant throughout the school year at 1 new case per hundred uninfected students per week. By the end of the forty-week school year, how many students would you expect to have contracted the disease? Use the formula for approximating the cumulative incidence from the incidence rate. Show your work.
7. Table 1 represents data from a study of 475 patients AIDS patients who were given a new treatment and followed over 8 years to determine survival.
a. Fill in all the numbers where the question marks are. More specifically, calculate the At Risk, Survived, and Kaplan-Meier Survival Probability Estimate values. Carry the results out to 3 significant digits.
|
Time (Years)
|
At Risk
|
Censored
|
Died
|
Survived
|
Kaplan-Meier Survival Probability estimate
|
|
1
|
475
|
27
|
96
|
379
|
?
|
|
2
|
?
|
13
|
55
|
?
|
?
|
|
3
|
?
|
2
|
55
|
?
|
?
|
|
4
|
?
|
3
|
25
|
?
|
?
|
|
5
|
?
|
6
|
15
|
?
|
?
|
|
6
|
?
|
8
|
20
|
?
|
?
|
|
7
|
?
|
6
|
10
|
?
|
?
|
|
8
|
?
|
3
|
5
|
?
|
?
|
b. What is the cumulative incidence of survival for the HIV patients receiving the new treatment at year 8?
c. What is the survival rate at year 4?
d. What is the cumulative probability of mortality?
8. Figure 1 represents data relapse-free survival curves for the lung cancer trial for two treatment groups. Data originate from a phase III clinical trial of 164 patients with surgically resected (non-small cell) lung cancer, randomized between 1979 and 1985 to receive radiotherapy either with or without adjuvant combination platinum-based chemotherapy (Lung Cancer Study Group, 1988; Piantadosi, 1997).
a. At year 4, what is the relapse probability for each treatment groups?
b. What is the relapse-free survival percentage for radiotherapy alone?
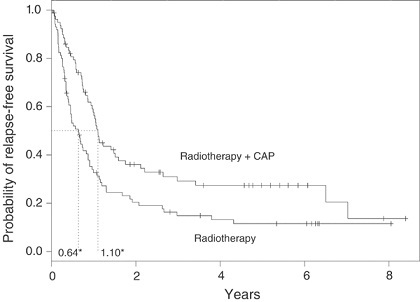
Figure 1. Kaplan-Meier Curves for question 8. Relapse-free survival curves for the lung cancer trial. * Median relapse-free survival time for each arm, + censoring times, CAP=cytoxan, doxorubicin and platinum-based chemotherapy.
c. Describe and interpret the two survival curves in Figure1? How would we test if the curves are significantly different? Is there an advantage of one treatment over another from the perspective of relapse? From the perspective of survivability?
9. In 2001, a total of 15,555 homicide deaths occurred among males and 4,753 homicide deaths occurred among females. The estimated 2001 midyear populations for males and females were 139,813,000 and 144,984,000, respectively.
A. Calculate the homicide-related death rates for males and for females.
B. What type(s) of mortality rates did you calculate in Question 9 A?
C. Calculate the ratio of homicide-mortality rates for males compared to females.
D. Interpret the rate you calculated in Question C as if you were presenting information to a policymaker.
10. Article Comprehension: Read the article by Dupre et al. JAMA Internal Medicine, 2012 The Cumulative Effect of Unemployment on Risks for Acute Myocardial Infarction.
1. Was the study cohort a fixed or dynamic cohort? Explain your answer.
2. What was the overall incidence of AMI in the study cohort?
3. Did the investigators measure cumulative incidence of AMI in the cohort? If so, what was it? If not, why not?
4. What was the mortality rate in the cohort (in person-years)?
5. What additional information would you need to determine the AMI case fatality rate?