Reference no: EM13800101

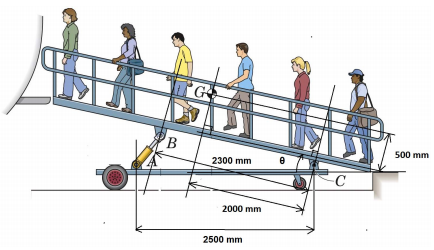
1. The ramp shown below is used to assist passengers boarding light commuter aircrafts. The average mass of the ramp and passengers is 800 kg with the center of mass located at point G. As the ramp angle θ increases, the hydraulic cylinder extends but the distance between the center of mass G and pivot C remains fixed.

a) Derive the equation for length AB as a function of BC, AC and θ.

b) Derive the equation for angle BAC as a function of BC, AB and θ.

c) Calculate the pivot reaction force (FC) and hydraulic cylinder force (FAB) at a ramp angle of 10 degrees.

d) Plot the variation of Fc and FAB as a function of θ over the range 10 < θ < 20.

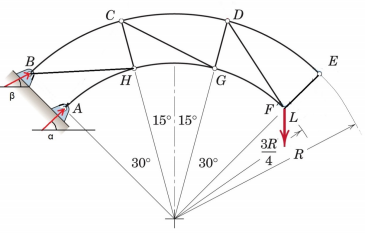
2. Consider the plane truss shown below. The reaction force at points A and B act at an angle of α = 30 and β = 22 degrees relative to the horizontal axis.

a) Determine the reaction forces at points A and B.

b) Determine the force in member AH.

c) Determine the force in members BH and BC.

d) Determine the force in members CH and HG.

e) Determine the force in members CD and CG.

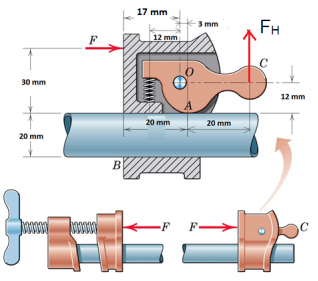
3. The pipe clamp ends are designed to fit a standard 20 mm steel water pipe. The right hand fitting can slide along the pipe when handle C is held up to release its grip on the pipe. When the handle is released and a clamping load of F = 1000 N is applied by the screw, the fitting makes contact with the pipe at points A and B. In this position, the spring is compressed with a spring constant of 400 N/mm. Assume that the handle is a frictionless surface.

a) Determine the static friction coefficient at point B needed to avoid slip under loading.

b) Calculate the force acting at point A and B under loading.

c) Estimate the compression of the spring under loading. Assume that the handle OC remains parallel to the pipe.

d) Calculate the handle force required to loosen the fitting.

e) Calculate the force supported by pin O when the above handle force is applied.