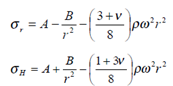Reference no: EM13939

Question 1

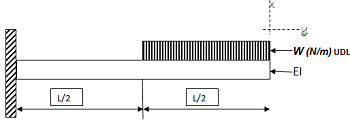
A cantilever beam of constant cross section carries a uniformly distributed load W (N/m) across half its span as shown in Figure Q1 below.

The deflected shape may be represented by the general polynomial:

y = a + bx + cx² + dx³

The general expression for the internal Elastic Strain Energy in each element is given by:

U =EI/2 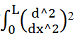dx

(N.B: in the part in the brackets above, it requires a division sign in there, ie d^2 / dx^2)

i). Using the general polynomial for the deflected shape given above, satisfy all known boundary conditions of deflection and rotation and then minimise the total potential energy of the system to determine a suitable expression for the deflection at the free end.

ii). If the entire length of the beam is 6m, its flexural rigidity is 200kNm² and the half span load per unit length is 1kN/m, calculate the free end deflection caused by the load.

Figure

Question 2

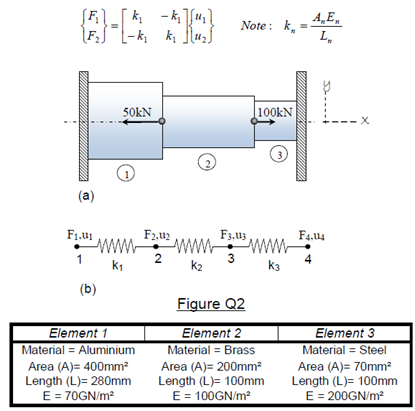
Three dissimilar materials are joined together to form a stepped bar arrangement and are placed between rigid end clamps as shown in Figure

Q2(a). The system may be represented by a model consisting of three discrete spring elements shown in Figure Q2(b).

If two concurrent, co-planar forces of 50kN and 100kN are applied at the interface between the materials, use a finite element method to calculate:-

i.) The displacement at node point 2 and 3. 

ii.) The forces exerted on the end clamps. 

The force-displacement equation for each element may take the form:-

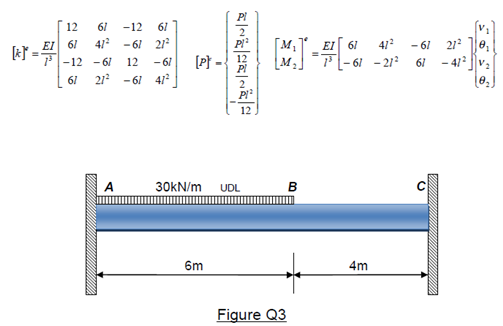
Question 3

Figure Q3 below shows a beam of constant cross section built in at both ends A and C. The beam is 10m long and carries a uniformly

distributed load of 30kN/m along a span of 6m at AB.

Use a finite element method consisting of two elements to:

i). Calculate the deflection at B. 

ii). Sketch the bending moment diagram showing the principal values.

For the model:

Flexural Stiffness EI = 800kNm²

Question 4

i). Show that for a thick walled cylinder of internal radius ri and external radius ro acting under an internal pressure P, the general expressions for radial and hoop stresses may be given by:

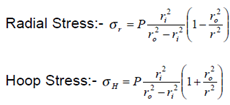
ii). The hydraulic power jack of an industrial press may be modelled as a compound cylinder which has a cast iron liner of bore 100mm and wall thickness 8mm pressed into an aluminium cylinder of wall thickness 16mm. The diametral interference is such to give an interface pressure of 10MN/m² on assembly.

Assuming the axial stress is zero (σ = 0) L s determine:-

a) The diametral interference.

b) The maximum allowable pressure in the cylinder, if the liner is to remain in compression.

iii). Comment on any design restrictions a compound vessel of this type might impose and give two other manufacturing techniques one can use to achieve improved stress distributions.

Take the following properties for cast iron and aluminium:-

Cast Iron                       Aluminium

E = 180GN /m²             E = 70GN /m²

nu = 0.3                         nu = 0.33

Question 5

A solid shaft has a coupling flange which consists of a thin steel ring shrunk onto a shaft. The axial thickness of the ring is sufficiently small to assume that a state of plane stress exists in the coupling. The shaft and ring have outside diameters of 440mm and 600mm respectively. The shaft normally runs at 2550 RPM and the coupling is to be designed such that the ring just becomes free at 15% over normal speed.

Calculate:

i. The maximum stresses in the shaft and ring at 15% overspeed. 

ii. The required diametral interference between the shaft and the ring.

iii. The interface pressure at normal running speed.

Properties of steel are:

E = 200GN / m²

nu = 0.3

r = 7800kg / m³

For a rotating disc: