Reference no: EM132610664

Assignment - General Properties of Matter

Question: [1] Show that the interaction energy between an ion with charge Q (say Li⁺) and a polar molecule(say H₂O) situated at a distance r from the center of the ion at an angle θ to the line joining two is given by

W (r, θ) = -Qu(Cosθ)/4πs0sr²

Where u is the dipole moment of the polar molecule.

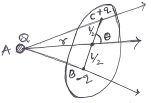
Calculate the maximum possible value of the P.E. given that the size of Li⁺ = 0.068 nm , dipole moment of water u = 1.85D and size of H₂O molecule ≈ 0.14 nm. Compare the value with the thermal energy KBT .

Question: [2] The Lennard Jones pair-potential function is used to approximate the van der waals interaction in closed shell atoms like Ar.
(i) Plot the net energy between two Ar atoms using the L-J potential function given as
V (r) = 4 ∈[(σ/r)¹² - (σ/r)⁶ ] plot for 2.5A⁰ < r < 8A⁰

(ii) On the plot indicate the equilibrium inter atomic distance r₀ and the bonding energy E₀ .

(iii) Solve for the bonding energy and equilibrium distance analytically and get the values for Ar. Given that σ_Ar = 3.405A0 and s_Ar = 1.032 × 10^-2eV .

(iv) How would the plot change for a material with a greater melting temperature ?

(v) Instead of neutral atoms, if we have the ionic bonds formed be- tween two ions, what will be the relationship between the energy due to the attractive force EA and the interatomic distance r ? what is the relationship between the energy due to repulsive force ER and the interatomic spacing ? Which force drops off quicker as r is increased ?

Question: [3] Resultant stress due to the combination of two simple stresses in di- rection perpendicular to each other.

(i) Consider a block of material subjected to a pair of stretching forces Fx, Fx ; Fy , Fy as shown below

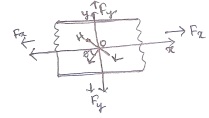
Calculate the normal and tangential stresses acting on any plane HK passing though O and the normal to the HK plane makes an angle θ with x- axis. Let px and py be the stresses produced at point O by the forces Fx and Fy. Show that the tangential stress is maximum when θ = π .

(ii) Suppose in the above problem the forces Fy are changed such that they tend to compress the material. Again calculate the normal and tangential stresses in such situation.

Question: [4] Let A and B be two points to which the ends of a horizontal wire of length 2l₀ are fixed.

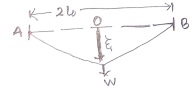
Let O be the mid-point of A and B and suppose that the wire is loaded centrally with weights W₁ and W₂ at the O, which produces a depression of ξ1 and ξ2 respectively to the wire. Show that the Young's modulus for the wire is given by

E = [(W₂/ξ₂ - W₁/ξ₁ ) l₀³/A]/(ξ₂² - ξ₁²)

Where A is the cross-sectional area of the wire.

Calculate the Young's modulus of a 1.0 m long steal wire with cross- sectional area 1 mm2, which sags to a distance of 5.0 mm when loaded with 40 gm. And a load of 600 gm makes a depression of 15 mm to the wire in the above arrangement.

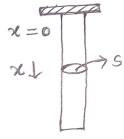
Question: [5] Let "S" be the cross-sectional area of a rod hanging vertically under it's own weight and let "l" be it's unstretched length. Show that the increment in the length of the rod, due to it's own weight is

ξ = 1/2.gρl²/E

where ρ is the density of the material and E is it's young's modulus

Question: [6] Consider a hollow cylinder of length l and of inner and outer radii equal to r₁ and r₂ respectively. Let the upper end of it be fixed and a couple is applied to the lowered end in a plane perpendicular to it's length, twisting it through an angle θ. Calculate the twisting couple of the cylinder. Compare the twisting couple per unit twist of the above hollow cylinder with a solid one (with radius r) made up of same material and having same mass and length.

Question: [7] In order to deform a body, work must be done by the applied force. Let F be the force applied to a wire, which is fixed at the upper end. The original length of the wire is L , 'a' is the cross-sectional area of the wire with Young's modulus Y. Calculate the work done per unit volume by the applied force during the stretch of the wire from 0 to l.

Question: [8] A bronze bar, 1.7m long and 50mm in diameter is subjected to a tensile stress of 70meganewton/m². Calculate the extension producedin the bar and the work done during the process. The value of Young's modulus for the material is 85 × 109N/m².