Reference no: EM13156764

Estimation and Testing of Capital Asset Pricing Model

 The capital asset pricing model (CAPM) is an important model in the field of finance. It explains variations in the rate of return on a security as a function of the rate of return on a portfolio consisting of all publicly traded stocks, which is called the market portfolio. Generally the rate of return on any investment is measured relative to its opportunity cost, which is the return on a risk free asset. The resulting difference is called the risk premium, since it is the reward or punishment for making a risky investment. The CAPM says that the risk premium on security j is proportional to the risk premium on the market portfolio. That is,

r_j - r_f = β_j(r_m - r_f)

where r_j and r_f are the returns to security j and the risk-free rate, respectively, rm is the return on the market portfolio, and β_j is the jth security's ''beta'' value.

A stock's beta is important to investors since it reveals the stock's volatility. It measures the sensitivity of security j's return to variation in the whole stock market. As such, values of beta less than 1 indicate that the stock is ''defensive'' since its variation is less than the market's. A beta greater than 1 indicates an ''aggressive stock.'' Investors usually want an estimate of a stock's beta before purchasing it. The CAPM model shown above is the ''economic model'' in this case. The ''econometric model'' is obtained by including an intercept in the model (even though theory says it should be zero) and an error term,

r_j - r_f = α_j + β_j(r_m - r_f) + e

Estimate the model for each stock. The corresponding Eviews outputs for all 6 regressions should be attached at the back of your report.

Finance theory suggest that αj = 0 under market efficiency. This is because αj represents excess profit or loss when the market excess return rm - rf = 0. That is, if αj > (<) 0, the stock consistently outperforms (underperforms) the market. However, if the market is efficient, this profit (loss) should disappear rather quickly by arbitrage.

1. Test the null hypothesis that αj = 0 for Microsoft, against an appropriate alternative hypotheses.

"Tech stocks typically have higher beta. An example is the dot-com bubble. Although tech stocks did very well in the late 1990s, they also fell sharply in the early 2000s, with a much worse decline than that of the overall market."

2. The above statement implies that Microsoft (a Tech stock) is an aggressive stock. Evaluate this claim by conducting an appropriate test on their β values.

"Mobil-Exxon" is an oil company with stable business conditions and should be a safer investment than the overall market"

3. The above statement implies that Mobil-Exxon is a defensive stock. Evaluate this claim by conducting an appropriate test on its β.

Based on the estimation results, fill out the following table:

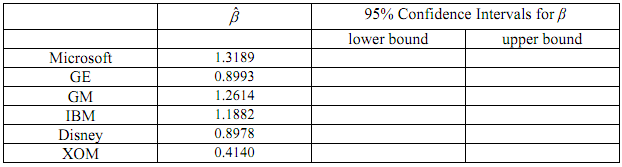
4. Show your working for all confidence intervals above.

5. Interpret the 95% confidence intervals for GE, GM, and Disney, paying attention to their risk profile (aggressive, defensive, neutral)

It is supposed that, for January 2009, the market return (rm) is expected to be either 0.05 (5%) with the probability 0.5; or -0.05 (-5%) with the probability 0.5. Assume the risk-free rate to be 0 and α values to be 0.

6. Calculate the expected returns and standard deviations from Microsoft and Mobil- Exxon stocks for January 2009. If you wish to minimize your risk (measured by standard deviation), which stock would be your preferred investment?

7. An investor is seeking your recommendation to invest in three stocks among the above. Her goal is to form a portfolio of three stocks with well-diversified risk profiles. State your recommendations and justify your choice in relations to the properties of β values found above.

"Using beta as a measure of relative risk has its own limitations. Most analysts consider only the magnitude of beta. Beta is a statistical measure and should be considered with the model's goodness-of-fit (R2 value of the regression). Higher R2 value implies a stronger relationship between stock return and market portfolio."

8. Critically evaluate the merit or otherwise of the above statement by commenting on the R2 values of the estimated CAPM regressions above.