Calculate the expected number of deaths for each chemical

Assignment Help Engineering Mathematics

Reference no: EM131524617

Question: A policy maker in the Occupational Safety and Health Administration is under pressure from industry to permit the use of certain chemicals in a newly developed industrial process. Two different versions of the process use two different chemicals, A and B. The risks associated with these chemicals are not known with certainty, but the available information indicates that they may affect two groups of people in the following ways:

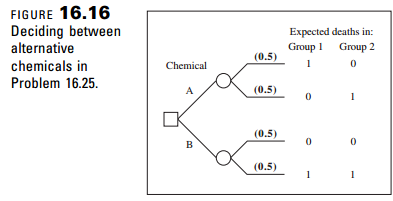
? Chemical A There is a 50% chance that Group 1 will be adversely affected, while Group 2 is unaffected; and a 50% chance that Group 2 is adversely affected, while Group 1 is unaffected.

? Chemical B There is a 50% chance that both groups will be adversely affected, and a 50% chance that neither group will be affected.

Assume that "adversely affected" means the same in every case-an expected increase of one death in the affected group over the next 2 years. The decision maker's problem looks like the decision tree in Figure.

a. Calculate the expected number of deaths for each chemical.

b. A decision maker who values consequences using an overall utility might calculate the utility for each consequence as
U(Chemical) = k1U1(Group 1 Deaths) + k2U2(Group 2 Deaths) For both U1 and U2, the best and worst possible outcomes are 0 deaths and 1 death, respectively. Thus,

U₁ (1 Death) = 0 U₁ (0 Death) = 1

U₂ (1 Death) = 0 U₂ (0 Death) = 1

Explain why k1 and k2 = 1 - k1 may not be equal

c. Assume that k1 = 0:4. Show that the decision maker who evaluates the two chemicals in terms of their expected overall utilities (as defined previously) would be indifferent between them. Does the value of k1 matter?

d. Why might the decision maker not be indifferent between the two programs? (Most people think about the decision maker's risk attitude toward the number of deaths or lives saved. Besides this, think about the following: Suppose you are a member of Group 1, and the decision maker has chosen Chemical A. It turned out that Group 1 was affected. How would you feel? What would you do? What does this imply for the decision maker?)

718_16.16.png

Reference no: EM131524617

Questions Cloud

Would it make sense to consider a direct switch : Refer to the discussion of the automobiles in the section on "Trading Off Conflicting Objectives: The Basics." We discussed switching first from the Standard.

Emotional attachment to the character or person : Explain any emotional attachment to the character or person. Have they disappointed you? Motivated you? How and why?

Write a research paper about environmental policies : Research and write an APA research paper about environmental policies.Summarize the major provisions of the law that you chose.

Ceos and presidents for a management journal : You have been encouraged by a colleague to write an article about "CEOs and presidents" for a management journal. You have decided to compare the leadership.

Calculate the expected number of deaths for each chemical : A policy maker in the Occupational Safety and Health Administration is under pressure from industry to permit the use of certain chemicals in a newly.

Describe the laws of thermodynamics : Describe the laws of thermodynamics.Explain how these scientific laws apply to energy use, energy conversions, and the need for energy efficiency.

Transportation service for our clients : I am thinking of establishing a cleaning service that also provides food service for our clients including transportation service for our clients.

The pollutant chosen and the source of the pollutants : Describe the pollutant chosen and the source of the pollutants. Include both natural and human sources, as applicable.

Important assets of an organization are its employees : The most important assets of an organization are its employees. Given the right opportunities and structure, employees will be empowered.

User Account

All Pages