Calculate the electric field around circles

Assignment Help MATLAB Programming

Reference no: EM132394444

COMPUTER LAB REPORTS

You are carrying out experiments in the computer lab! The difference is the experimental kit is actually lines of code in MATLAB and so the results are numbers generated by that code.

Your report will therefore follow the same format as that of the lab report you submitted in week 8, with only a few subtle differences.

Abstract and introduction/background are as for a regular lab report.

The methods section must contain a summary of the MATLAB code, including the input given to the MATLAB code and the format of the output produced, what a typical run looks like, a description of the calculations carried out etc.

Results and discussion are as for a regular lab report. Don't forget that MATLAB code has "errors" (or perhaps "bugs") too. Does the MATLAB code solve the problem correctly compared to theory? Describe the tests you carry out to verify the output of the code.

Conclusions are as for regular lab report, however this time you would suggest improvements to the program rather than the benchtop experiment.

References as for regular lab report.

Report 1

Background: The code is written to calculate the electric field around circles that are, in fact, infinitely long rods with circular cross section and not spheres or discs. For example, a very small charged point represents the cross section of a thin charged wire rather than a charged particle.

You will test whether the electric field output from the MATLAB code better describes the small particle (vanishingly small in z direction) or small wire (infinite in z direction) scenario. You will then test how accurately it simulates other theoretically predictable features of the electric field.

Suggested procedure: What is the theoretical electric field around a charged particle? What is the theoretical electric field around a line of charge with a charge density of λ C/m? (Use Gauss' law if necessary to obtain these expressions). Note in particular the different dependence of the electric field on distance for these two charge geometries.

Use the MATLAB code to calculate the electric field around a "small" charge. Export the electric field strength as a function of x position, import it into another package you are familiar with and plot it. Fit the calculated electric field. What function of position fits best - the function that describes the electric field around a point charge or a line charge?

Increase the diameter of the charged rod and assume the charge in the rod is uniformly distributed over its cross section. Compare the theoretical electric field distribution inside the wire (use Gauss' law if necessary) with that calculated by MATLAB once again by fitting.
What is the physical significance of the divergence of the electric field? Determine the analytical expressions for the curl of the electric field outside and inside the rod and compare your expressions with those expected from Faraday's law in differential form. Compare your expressions with those calculated in MATLAB.

Report 2

Background: The code is written to calculate the magnetic field around finite length conductors carrying constant currents with a uniform current density.

You will test how accurately it simulates theoretically predictable features of the magnetic field. You will also use it to comment on the effect of the finite length of the conductor on the magnetic field.

Suggested procedure: What is the theoretical magnetic field around a current-carrying conductor which is an infinitely long cylinder? What is the theoretical magnetic field around an infinitely long solenoid or planar sheet? (Use Ampere's law to obtain these expressions). Note in particular the different dependence of the magnetic field on position for the two current geometries you have chosen.

Use the MATLAB code to calculate the magnetic field in 3 dimensions around the two geometries you have chosen (the tube is a good approximation of a solenoid). Note that the MATLAB simulation is for conductors of finite length only. Export the magnetic field strength as a function of position.

You may need more than one plot to completely describe the magnetic field in 3 dimensions. Plot the magnetic field(s) as a function of position in a plane at the centre of the conductor lying perpendicular to the length of the conductor (see below for example).

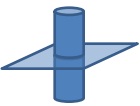
2172_Image 1.jpg

Fit the calculated magnetic field. Do the fields calculated using Biot-Savart law match those predicted by Ampere's law?

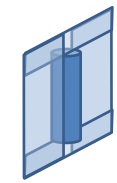
2322_Image 2.jpg

Plot magnetic field strength as a function of position in a plane centred on the origin and extending along the length of the conductor. Comment on what happens to the magnetic field as you move away from the centre of the conductor towards the ends. Over what fraction of the length of the conductor can the magnetic field be "well" approximated by the expression for the infinitely long conductor? (You will need to assign a value to "well"!)

The plots of ∫ B^→ . dl shows the magnetic field evaluated around circular Amperian loops of increasing radius. Compare these results with those predicted by the current enclosed by the loops.

Reference no: EM132394444

Questions Cloud

Public health law and individual rights : Ethical questions and issues arise at both the level of setting laws and policies and the level of deciding what to do where, those are indeterminate.

Traditional analysis has looked at make versus buy : Traditional analysis has looked at make versus buy alternatives, but recently firms have begun to consider partnerships or strategic alliances as a third

Hospital ended up rehiring its employees anyway : In the housekeeping situation, why not just forget about outsourcing, especially since the hospital ended up rehiring its employees anyway?

Outsourced work performed within the hospital : What advantages were there in having the outsourced work performed within the hospital?

Calculate the electric field around circles : Does the MATLAB code solve the problem correctly compared to theory? Describe the tests you carry out to verify the output of the code.

Psychological and social history is holistic approach : Assessing a client's biological, psychological, and social history is a holistic approach that is an essential aspect of social work practice.

Toronto Historical Labour Sites - Research Assignment : Toronto Historical Labour Sites: Research Assignment. Part 2: Research Report. The research component: your report on the history and significance of the site

Determine the expectations you have for yourself as a leader : The practice scholar works in a space between action and potential, anticipating the next step and translating the process for others. They bring the vision.

What would be the total estimated hourly cost : Who is paid $30 per hour and can process 16 arrivals per hour. Which attendant should be selected, and what would be the total estimated hourly cost?

User Account

All Pages