Calculate the displacement from equilibrium

Assignment Help Mathematics

Reference no: EM131806930

Q1 Solve the first order homogeneous differential equation dy/dx = (2x - y - 4)/(x + 2y -5)

Q2 Let f(x, y) = e^5x siny, find the Taylor series expansion of the function f(x +1/4, y + Π/3) in the form = e^5x(A sin y+ B cos y)i.e. find A, B

Q3 If y = e^6x sinx using Leibnitz's theorem on repeated differentiation, or otherwise show that

d⁴y/dx^{4 =}e^6x{1081 sinx + 840cosx}

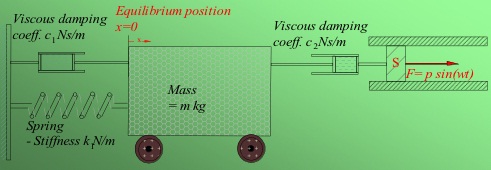
Q4 The spring-mass-damped system shown in Fig 1, has data m = 0 kg, k =1800 Nm^-1 c₁= 650 Ns m^-1 c₂ = 700 Ns m^-1 w =10 , p =14, and initial conditions x(0). x^.(0), = 0.15ms^-1

Using the relationship sin(wt) e^iwt -e^-iwt , and the differential operator, calculate the displacement from equilibrium position function x(t).

Reference no: EM131806930

Questions Cloud

Subsequent payments will increase at a uniform : Subsequent payments will increase at a uniform 10% rate each year (second payment is $1210; third payment.

Prepare in good form a multiple-step income statement : Income taxes are calculated at 30 percent of income. Prepare in good form a multiple-step income statement for Mid City Galleries

How much must Helen set aside in savings account : Helen pays rent of $400 per month for the academic year (September through May). She is going to Australia for the summer and won't be working.

Would you recommend that the pipeline be installed : Fifteen families live in Willow Canyon. Although several water wells have been drilled, none has produced water. The residents take turns driving a water

Calculate the displacement from equilibrium : Solve the first order homogeneous differential equation - sinx using Leibnitz's theorem on repeated differentiation

Determine how much each class of stock should receive : Determine how much each class of stock should receive under each of the conditions stated.

What rate of return did he receive on his investment : He received no dividend for the ninth year. At the end of the ninth year he sold his stock for $6000. What rate of return did he receive on his investment?

What is the pw of the given cash flows : What is the PW of the following cash flows? $2800 for the first year and decreasing by $150 for each of the next eight years at 8%.

Prospect of improved future earnings : One aspect of obtaining a college education is the prospect of improved future earnings in comparison to non-college graduates.

User Account

All Pages