Calculate the dimensions of the equivalent flat plate

Reference no: EM131515314

Question: Dolphins have been observed swimming at sustained speeds of up to 11 m/s. According to the distinguished zoologist Sir James Gray, this speed can be achieved, assuming normal hydrodynamic conditions prevail, only if the power produced per unit mass of muscle far exceeds that produced by other mammalian muscles. This result is known as Gray's paradox. The object of this exercise is to revise estimates of the power required to check the soundness of Gray's calculations. Assume that the dolphin's body is hydrodynamically equivalent to a prolate spheroid (formed by an ellipse rotated about its major axis) of 2 m in length with a maximum thickness-to-length ratio of 1:6.

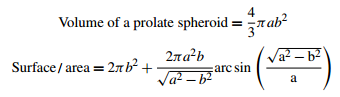
where 2a is the length and 2b is the maximum thickness.

Calculate the dimensions of the equivalent flat plate and estimate the power required to overcome the hydrodynamic drag (assuming it to be solely due to skin friction) at 11 m/s for the following cases:

(a) Assuming that the transitional Reynolds number takes the same value as the maximum found for a flat plate, say 2 × 106

(b) Assuming that transition occurs at the point of maximum thickness (i.e., at the point of minimum pressure), which is located halfway along the body

The propulsive power is supplied by a large group of muscles arranged around the spine. Typically their total mass is about 36 kg, the total mass of the dolphin being typically about 90 kg. Assuming that the propulsive efficiency of the dolphin's tail unit is about 75%, estimate the power required per unit mass of muscle for the two cases (a) and (b). Compare the results with the values given here:

• Running man, 40 W/kg.

• Hovering hummingbird, 65 W/kg

Reference no: EM131515314

Questions Cloud

Explain why the letter writers logic is faulty : Many years ago Scientific American published a letter about the aerodynamics of pollen spores. A photograph accompanied the letter showing a spore.

Bond is a premium bond making semiannual payments : Bond X is a premium bond making semiannual payments. What do you expect the prices of these bonds to be in twenty years?

The ability to validate image and file integrity : The ability to validate image and file integrity.The ability of identifying dates and times that files have been modified, accessed and created.

Calculate the required return and expected return for stock : Calculate the required return and expected return for this stock.

Calculate the dimensions of the equivalent flat plate : Dolphins have been observed swimming at sustained speeds of up to 11 m/s. According to the distinguished zoologist Sir James Gray, this speed can be achieved.

Consider arbitrageur who does not hold any position in zinc : Consider arbitrageur who does not hold any position in zinc. Show how this arbitrageur could make an arbitrage profit when the 90-day forward price is US$1865

Cross-border acquisitions over greenfield investments : Which of yhe following is NOT an advantage of cross-border acquisitions over greenfield investments?

What is reward-to-risk ratio for market portfolio and stock : What is the reward-to-risk ratio for the market portfolio and Stock Z?

Estimate the coefficient of skin-friction drag : The top surface of a light-aircraft wing traveling at an air speed of 55 m/s is assumed to be equivalent to a flat plate of length 2 m.

User Account

All Pages