Reference no: EM132544626

Revision Quiz

Question 1. Suppose that X, Y, Z are random variables such that Y = E[X | Z]. Show that

Var(Y ) ≤ Var(X).

Question 2. Let A be an n x n matrix and X an n-dimensional random vector with expectation µ and covariance matrix Σ. Show that

E[X^TAX] = µ^TAµ + tr(AΣ).

Question 3. Suppose that

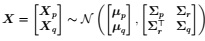
Show that

X_q + Σ_r^T Σ_p^-1(x_p - X_p)

has the same distribution as (X_q | X_p = x_p) (the distribution of X_q, con- ditional on X_p = x_p).

Hint: Write

X_q - Σ^T_r Σ_p^-1X_p = -Σ^T_r Σ_p¹, I_q] X

and calculate the covariance matrix of the right-hand side.

Time Series Quiz Questions

Question 4. Let W_t ∼iid N(0, 1) and define the process
X_t := W_tS_t-1, t = . . . , -1, 0, 1, . . .
where S_t := sign(Wt). In answering the following questions you must pro- vide adequate reasons and/or mathematical proofs of your assertions.

(a) Is X_t a weakly stationary white noise time series? (You must com- pute the means, variances and autocovariances as part of your answer.)
(b) Is {X_t} a strictly stationary process?
(c) Is {X_t} ∼iid N(0, 1)?

Question 5. Let Zt ∼iid N(0, 1) and define the process
Xt = ZtZt-1, t ∈ Z .
(a) Is {Xt} a weakly stationary time series? To establish this you will need to calculate the mean and covariance functions for {Xt}.

(b) Is Xt strictly stationary? A sequence of identically distributed random variables?

(c) Is {Xt} a Gaussian process? Give reasons.

(d) Let Wt = Xt² be the squared process. Show that EWt = 1, Var(Wt) = 8, Cov(Wt, Wt+l) = 0 for |l| > 1 and Cov(Wt, Wt+l) = 2 for |l| = 1.

(e) Calculate the autocorrelations for the squared process {Xt²}.

Question 6. Let An be a tridiagonal covariance matrix. Write pseudocode for the LDL factorization of An in (n) time. Implement it in R/Matlab/Python and test that it works for n = 10. Next, write pseudocode for solving the linear system Anx = bn for some bn in (n) time. Then, implement this code on a computer and test it.

As a test matrix, you may use the following Matlab generated matrix

A=diag(1:10)+diag(9:-1:1,-1); A=A‘*A.

Question 7. Verify that if Ln is a lower triangular matrix with ones down the main diagonal, then its inverse L_n^-1 is also a lower triangular matrix with ones down the main diagonal.

Question 8. Show that γ(t, s) = min{t, s} is a valid covariance function.

Question 9. Using the spectral results about the autocorrelation in lectures, explain whether 2 exp(-2|t| ) can be (or cannot be) a valid autocovariance function of a stationary process. Give reasons/proofs.

Question 10. Let X₁, X₂ be random variables with mean zero, unit variance, and covari- ance Cov(X₁, X₂) = 0. Consider the time series for β ∈ (-π, π):

Yⁿ = X¹ cos(nβ) + X² sin(nβ), n ∈ Z .

Give a formula for the spectral density of Y_n using the delta function

δ(x) = 0  x ≠ 0 .
δ(x) = ∞, x = 0

Question 11. Let U~U(π, π) and V ~ fV (v) be independent (fV is a pdf). Show that the time series

X_t := exp(iU - iV t), t ∈ Z

is stationary and find its spectral pdf.

Question 12. Let {X_t} be a weakly stationary time series with mean µ and continuous spectral pdf f. Define the average X_t = X1+.....+X_t . Show that

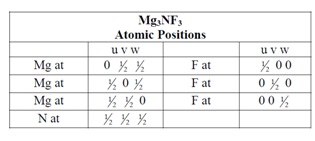
is the so-called Fejer kernel with the property that

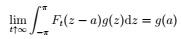
for any continuous function g. Hence, conclude that tVar(X¯t) → 2πVar(X1)f˜(0) and X¯t -→ µ.

Question 13. Show that the inverse of F/√n, where

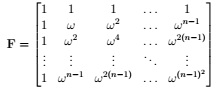
and ω = exp(-i 2π/n), is simply its complex conjugate F/√n.

Question 14. Complex-valued Multivariate Normal. Show that the joint density of (R, I) produced by the circulant embedding method can be written as:

f_Z(z) = 1/(2π)2n|C|² exp( -z^TC^-1z),

where Z := R + iI.

Question 15. Sunspot Data. Get the sunspot data from the course webpage and, using your own FFT implementation in Python/Matlab/R, compute and plot the power spectrum to obtain the picture in the lecture notes.

Question 16. Fractional Wiener Noise. A fractional Wiener noise Wt is a stationary Gaussian process with autocorrelation:

ρ(t) = |t + 1|^2h - 2|t|^2h + |t - 1|^2h/2 , t ∈ Z,

where h (0, 1) is the Hurst parameter. Write code to generate a fractional Wiener noise with Hurst parameters h = 0.2 and h = 0.95, and with length n = 104. Implement both an FFT spectral approach and an LDL decomposition approach for the simulation. Comment on the jaggedness of the timeseries.

Question 17. Fractional Brownian Motion. A fractional Brownian motion B_t is a nonstationary Gaussian process with correlation:

ρ(s, t) = |s|^2h - |t - s|^2h + |t|^2h/2 , t, s ∈ Z.

Show that the increment process defined as W_k:= B_t+k B_t is stationary and find a formula for its autocorrelation. How can you simulate this process given the previous problem?

Note: FIRST 10 Questions only