Reference no: EM132995093
PREDICTABILITY OF EXCESS RETURNS
Your tasks are as follows:
o Go back to the monthly simple return time series for U.S. Treasury bills maturing in three months you downloaded in exercise one. This will be our proxy for the risk-free rate, Rif , in this task. Import the data into R without modifying the files you downloaded. Aggregate the monthly simple return time series to an annual simple return time series. Calculate the simple gross return of the risk-free rate, 1 + Rf . Restrict your sample to post war data, i.e., from 1947 to 2020.
o Follow the steps outlined in Appendix B.6 and download the two monthly time series for the U.S. stock market index. Import the data into R without modifying the files you downloaded. Denote the simple value-weighted return including all distributions (e.g., dividend payments) by Rt and the one excluding all distributions by Rf . Aggregate each monthly simple return time series to an annual simple return time series.
Calculate the gross returns for Rt and RT:
1+Rt = pt+dt/(pt-1) and 1+Rxt = pt/pt-1
From 1 + Rt and 1 + Rtx we can back out the dividend-price ratio (also known as the dividend yield):
1+Rt/1+Rxt - 1 = (pt+d/pt-1)/(pt/pt-1) -1 = (pt+dt)/pt -1 = (pt+dt - pt)/pt = dt/pt
Calculate the (arithmetic) mean and the standard deviation of the dividend-price ratio in your sample.
o From the literature, it is known that this dividend-price ratio has some explanatory power for future excess returns (see, e.g., Fama and French (1988)). To check whether you can confirm this result, determine the market excess return in year t + 1 by subtracting the gross risk-free rate from our proxy for the market return, Rt+1:3
Rt+1 = α1 + β1dt/pt + u1,t
Calculate the (arithmetic) mean and the standard deviation of the market excess return in your sample. For this calculation, ignore any NAs in your time series.
o Use the dividend-price ratio in year t, -4, as independent variable, the market excess return in year t + 1 as the dependent variable, and run the following regression:
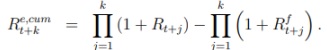
Put differently, you are studying, for instance, whether the dividend-price ratio in 1947 tells you something about the market excess return in 1948.
Report the parameter estimates, standard errors, and the R2 in your solution paper. Calculate the t-stats. Are the parameter estimates statistically significantly different from zero at the 5% level? Go through all steps of the corresponding test. For those that are statistically significant, explain its economic significance.
o To extend your analysis from the one-year horizon (k = 1) to the k-year horizon (for k = 3 and 5), calculate the corresponding cumulated excess return, R4er. That means, cumulate the gross market return over the next k years and subtract from this the cumulated gross risk-free rate over the same time span:
For k = 3 and k = 5, calculate the (arithmetic) mean and the standard deviation of the corresponding cumulated excess return. For this calculation, ignore any NAs in your time series.
Use the dividend-price ratio in year t as the independent variable, the cumulated excess return in year t k as the dependent variable, and run the following regression:
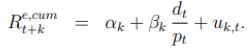
Put differently, for k = 3, you are studying, for instance, whether the dividend-price ratio in 1947 tells you something about the cumulated market excess return in 1950 which has been calculated over the years 1948, 1949, and 1950. For k = 5, you are studying whether the dividend-price ratio in 1947 contains information about the cumulated market excess return in 1952 which has been calculated over the years 1948, 1949, 1950, 1951, and 1952.
For k = 3 and k = 5, report the parameter estimates, standard errors, t-stats, and the R2 in your solution paper.
Attachment:- PREDICTABILITY OF EXCESS RETURNS.rar