Reference no: EM13160878

Question 1:

The surface is defined by the following equation:

z(x, y) = (3 + cos 2x)e^1+y3 + 5xy² - 6.

Find the equation of the tangent plane to the surface a.t the point P(0, -1).

Question 2.

Find all critical points of the function f(x, y)= In (x + y) + x² - y+ 64 and determine their character, that is whether there is a local maximum, local minimum, saddle point or none of these a.t each critical point.

Question 3.

Calculate the double integral by transferring to polar coordinates:

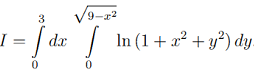
Make a sketch of the domain of integration. Present your answer in exact form and then evaluate it using a calculator up to two decimal places.

Question 4.

Evaluate the work done by the vector field

 

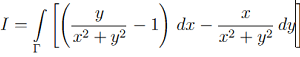
between the points A(Π/6,Π/6) and B(-Π,Π). Make an independent deci­sion about the most convenient path of integration τ. Present your answer in exact form and then evaluate it using a calculator up to two decimal places. 

Question 5.

Find the total electric charge Q of the plate D : {0 < x < 7r; 0 < y < 7r/2} if the surface density of the charge is:

q(x , y) = x sin (x + y).

Present your answer in exact form and then evaluate it ming a calculator up to two decimal places.

All quantities are presented he in the dimensionless form.

Question 6.

Find the total mass M of the wire if its line density is p(x,y, z) = x² -y² + z². The vector equation of the wire is

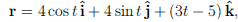
where 0 < t < Π/4.

Present your answer in exact form and then evaluate it using a calculator up to two decimal places.

All quantities are presented here in the dimensionless form.

Question 7.

Evaluate the integral of the vector field

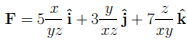
along the line r:

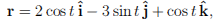
where t varies from Π/6 to Π/4. Present your result in exact form and eval­uate it up to two decimal places.

Question 8.

For the given vector field

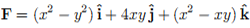
compute:

(a) the divergence in the point P(1, 2, 3);

(b) curl in the point P(1, 2, 3).