Reference no: EM13886773
1. A particle whose mass is 4.0 kg moves in the xy plane with a constant speed of 9.0 m/s along the direction of the vector (i^-j^) . When it is at the position (4.0 m, 0) calculate the angular momentum of the particle relative to the point (2.0 m, 0).
2. A 10 kg disk of radius 50 cm rotates while experiencing a variable torque given by ζ=(3.0t-2.0)N m . At time t = 2.0 s, its angular momentum is . At t = 5.0 s calculate the disk's
a. angular momentum
b. angular speed
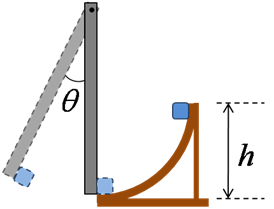
3. A small 60 g block slides down a frictionless surface through a height cm and then sticks to the lower end of a vertical rod of mass 150 g and length 50 cm. The rod pivots about a point near its upper end through an angle θ before momentarily stopping. Find θ.
4. A 32.0 kg child sits near the edge of a rotating merry-go-round that has the shape of a uniform disk of mass 60.0 kg and diameter 2.00 m. When the rotational speed is ω = 1.00 rad/s, the child catches a ball of mass 0.500 kg thrown by her mom. Just before the ball is caught, it hasa horizontal velocity of magnitude v = 16.0 m/s at an angle θ = 30.0° with a line tangent to the outer edge of the merry-go-round, as shown. Calculate the angular speed of the merry-go-round just after the ball is caught.
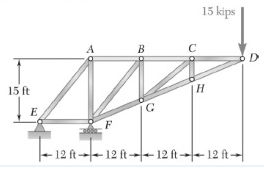
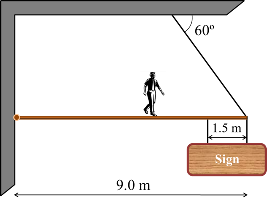
5. A horizontal beam of length 9.0 m and mass 30 kg is hinged at the wall, with the far end supported by a cable that makes an angle of 60° with the horizontal. A 20 kg sign hangs from the beam by two cables as shown. The cable can sustain a maximum tension of 900 N. A
76 kg man starts at the hinge and walks on the beam towards the sign. Calculate:
a. the maximum distance the man can walk safely
b. the reaction forces at the hinge just before the cable breaks
6. Two ladders, 4.0 m and 3.0 m long, are hinged at point A and tied together by a horizontal rope 75 cm above a frictionless surface, as shown. The mass of the longer ladder is 30 kg and that of the shorter one is 20 kg.
a. Calculate the upward reaction forces at the bottom of each ladder.
b. Calculate the tension in the rope.
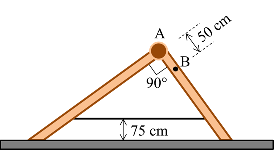
c. If a 78 kg painter stands at point B, what is the tension in the rope?
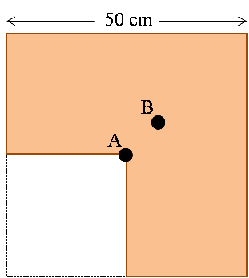
7. A square ceramic tile of side width 50 cm is prepared to fit around an edge. A square section of side length 25 cm is cut from one corner of the tile, as shown. As a result, the centre-of-mass of the tile shifts from point A to point B. Find the distance between these two points.
8. A satellite has a circular orbit with a period of 62 hours and a radius of km around a planet of unknown mass. If the magnitude of the gravitational acceleration on the surface of the planet is , calculate the planet's radius.
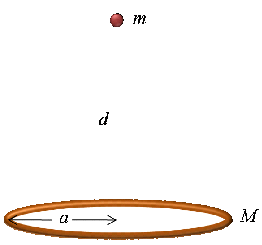
9. A particle of mass m is placed at a point along the axis of a ring at a distance d from its centre, as shown. The ring has a mass M and radius a.
a. Calculate the gravitational potential energy of the system.
b. Show that when the gravitational potential energy reduces to that between two point particles.
10. A weightlifter can lift 120 kg on the earth. What mass could the same person lift on
a. the moon?
b. the sun?