Reference no: EM1374968

1. In this exercise we will be building regression models for predicting house prices. We will be using data collected on 91 houses in Gainesville, Florida. The dataset contains the selling price of each house and information on four other explanatory variables.

The variables contained in the dataset are:

Y: Price. It is measured in thousands of dollars.

X₁: Area. It is the floor area of the house measured in thousands of square feet.
X₂: Bed. The number of bedrooms of the house.
X₃: Bath. The number of bathrooms of the house.
X₄: Pool. Indicates whether the house has a swimming pool.

Questions:
(a) Exploratory part.

i) Plot each of the predictors against the response. Plot the predictors against each other. The purpose here is to get a graphical idea of the relationships in the data. Do not include these plots in your report, just provide a brief summary of what you observed.

(b) Simple linear regression.

i) Fit 3 simple linear regression models with area, bed, and bath as the only predictor in each. Report the estimated parameters from the model that you consider to be the most useful in predicting house prices, along with an explanation why you consider that model to be the most useful one.

ii) Assuming that the best single predictor model is area, provide a 99% confidence interval for the mean price for a house area = 2500 square feet.

iii) Assume your neighbors own a house with area = 2500 square feet. Obtain a 99% prediction interval for the selling price of the house if they decided to sell it.

(c) Multiple linear regression.

i) Fit a regression model using all 4 predictor variables. Report the estimated i parameters and interpret the coefficient for the variable Pool.

ii) Suppose your neighbors house actually has area = 2500 square feet, 3 bedrooms, 3 bathrooms, and a pool. What is the predicted selling price for this house? Obtain a 95% prediction interval.

iii) Conduct an ANOVA P-test and interpret the results. Conduct a test to sec if the number of bedrooms a house has is a useful predictor of its price. Interpret the results. Should we include number of bedrooms in a model with the other 3 variables in it?

iv) Return to the model in (1) and use that as the full model. Fit a model without the variables pool and bath and use that as your reduced model. Conduct the F-test to see whether or not pool and bath are useful predictors using the full and reduced model. Interpret.

2. Let X₁,. .. , X_n. denote a random sample from a normal distribution with mean μ and variance σ². The probability density function (pdf) of X_i, i = 1, .. . , n, is given by

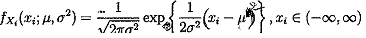
(a) Derive Derive the likelihood and log-likelihood functions.

(b) Show that the arithmetic mean, X', is the maximum likelihood estimator of the unknown mean μ.

(c) Show that the arithmetic mean, X', is a sufficient statistic for the unknown mean μ.
(d) Show that the sufficient statistic from part 2c is distributed as X'~N(μ,σ²/n).

(e) Use the pdf from part 2d to show that the arithmetic mean, X' is the maximum likelihood estimator of the unknown mean μ.