Reference no: EM13887507
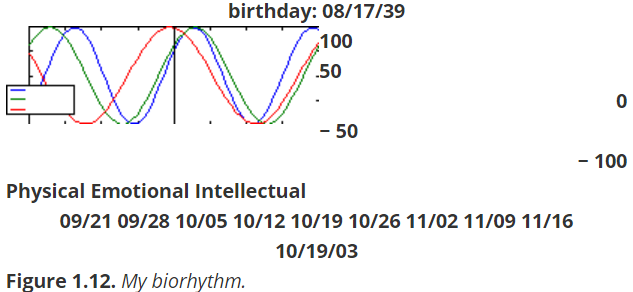
Biorhythms were very popular in the 1960s. You can still ?nd many Web sites today that o?er to prepare personalized biorhythms, or that sell software to compute them. Biorhythms are based on the notion that three sinusoidal cycles in?uence our lives. The physical cycle has a period of 23 days, the emotional cycle has a period of 28 days, and the intellectual cycle has a period of 33 days. For any individual, the cycles are initialized at birth. Figure 1.12 is my biorhythm, which begins on August 17, 1939, plotted for an eight-week period centered around the date this is being written, October 19, 2003.
It shows that my intellectual power reached a peak yesterday, that my physical strength and emotional wellbeing will reach their peaks within 6 h of each other on the same day next week, and that all three cycles will be at their low point within a few days of each other early in November. The date and graphics functions in Matlab make the computation and dis- play of biorhythms particularly convenient. Dates are represented by their date number , which is the number of days since the zeroth day of a theoretical calendar year zero. The function datenum returns the date number for any given date and time. For example, datenum('Oct. 19, 2003') is 731873. The expression fix(now) returns the date number of the current date.
The following code segment is part of a program that plots a biorhythm for an eight-week period centered on the current date.
t0 = datenum(mybirthday);
t1 = fix(now);
t = (t1-28):1:(t1+28);
y = 100*[sin(2*pi*(t-t0)/23)
sin(2*pi*(t-t0)/28) sin(2*pi*(t-t0)/33)];
plot(t,y)
1. Complete this program, using your own birthday, and the line, datetick, title, datestr, and legend functions. Your program should produce some- thing like Figure 1.12.
2. All three cycles started at zero when you were born. How long does it take until all three simultaneously return to that initial condition? How old were you, or will you be, on that date? Plot your biorhythm near that date. You should ?nd the lcm function helpful.
3. Is it possible for all three cycles to reach their maximum or minimum at exactly the same time?
|
Approach for effective project management
: The retrospective survey like other surveys offers a degree of information gathering as well as accountability. In this week's discussion consider how and when you would use this approach?
|
|
Linear temperature gradient and for simplicity
: The properties of the glass are α = 1.5 × 10-6/?C, E = 70 GPa, υ = 0.30. [Hint: Assume a linear temperature gradient and for simplicity take the midpoint strain as zero.]
|
|
What factor outside control of external auditor affect audit
: What factors outside the control of the external auditor affect audit quality? Why do users care about audit quality? Are there certain users who might care more about audit quality than others? Explain.
|
|
Fundamental to project risk management
: Identify two metrics that are important for you when working on a project and substantiate your answer using a practical example and credible academic or scholarly sources.
|
|
Biorhythm- matlab problem
: All three cycles started at zero when you were born. How long does it take until all three simultaneously return to that initial condition? How old were you, or will you be, on that date? Plot your biorhythm near that date. You should ?nd the lcm ..
|
|
Preemptive strikes
: Preemptive Strikes We've read both sides of the issue of whether or not the United States is justified in conducting preemptive strikes. But really, this is about us making decisions for ourselves and justifying it (or not) to the rest of the world.
|
|
How much work does friction do between point a and b
: At point A the wooden block below is traveling at 2.3 m/s. The coefficient of kinetic friction between the level table and the block is 0.22. How much work does friction do between point A and point B (just before it hits the floor)
|
|
Difference between euro fx futures and eurodollar futures?
: What's the difference between Euro FX futures and Eurodollar futures?
|
|
Surface of a ceramic material
: Rapid heating and cooling can cause cracks to start at the surface of a ceramic material. Sometimes the cracks meet the surface at 90? and sometimes at 45? to the surface.
|