Reference no: EM13537321
1. Consider the following Bayesian game. Nature chooses the type θ of player 1 from the set {1, 2, 3, 4} where each type has equal probability. Player 1, the sender, observes his type and may send a costless message from the set {m1,m2,m3,m4}, that does not affect either player's payoffs.. Player 2, the receiver, does not observe player 1's type, and must choose an action a from the set of real numbers. The sender's payoff is given by
U(θ,a) = 1.5a - (a-θ)2
The receiver's payoff is given by
V(θ,a) = - (a-θ)2
a) Show that there is always an equilibrium where the sender plays the same action after every message. Interpret this equilibrium.
b) Show that there cannot be an equilibrium with full separation of types.
c) Solve for an equilibrium with partial separation of types. (Hint. Look for separation between unequally sized subsets of the set of types).
d) Provide an argument why there cannot be any other equilibrium with partial separation apart from the one you find in part (c).
2. Firm A (the "acquirer") is considering taking over firm T (the "target").
It does not know firm T's value, it believes that this value, when firm T is controlled by its own management, is at least $0 and at most $100, and assigns equal probability to each of the 101 dollar values in this range. Firm T will be worth 50% more under firm A's management than it is under its own management. Suppose that firm A bids y to take over firm T, and firm T is worth x (under its own management). Then if T accepts A's offer, A's payoff is 3=2x y and T's payoff is y, if T rejects A's offer, A's payoff is 0 and T's payoff is x.
Model this situation as a Bayesian game in which firm A chooses how much to offer and firm T decides the lowest offer to accept. Find the Nash equilibria of this game. Explain why the logic behind the equilibrium is called adverse selection.
3. John Harsayni showed that a mixed strategy equilibrium of a perfect information game can be thought of as an approximation to an equilbrium (i.e. Bayesian NE) of a game where each player has a slight amount of incomplete information about the exact preferences of the other players. Consider the following Bayesian game, with payoffs as given below.
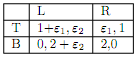
Nature chooses ε1 and ε2 independently, and both of these are uniformly distributed on the interval [-k, k] where k < 0.5. Player i is informed of the realization of εi, but not of εj, j ≠ i. Players then choose actions simultaneously.
a) Solve for an Nash equilibrium of this game when k = 0.
b) Solve for a Bayesian NE when k > 0, k < 0.5. What is the probability assigned by player i to the event that his opponent plays his first action in this BNE?
c) What do the probabilities in (b) converge to when k → 0. Interpret your results.
4. Consider the following simplified version of a game of poker. There are two players and three cards in a deck. Jack, Queen and King of spades. Player 1 always gets a Queen. Player 2 gets a Jack with probability 0.5 or a King with probability 0.5. In the first round, player 2 can either Raise or See. If he plays See, the game ends and players see each other's cards. Whoever has a lower card has to pay $1 to the opponent. If player 2 played Raise, the game continues to the second round in which player 1 can either play Pass or Meet.
If he plays Pass, the game ends and player 1 has to pay $1 to player 2. If player 1 plays Meet, the game ends and the players see each other's cards. Whoever has a lower card has to pay $2 to the opponent.
a) Formulate the game in the extensive form and draw a tree of the game.
b) What is an assessment in this game? Write it down in a parametric form (i.e. by denoting unknown strategies and beliefs by some letters).
c) Under what conditions on the belief system does player 1 play Meet?
d) Solve for all weak sequential equilibria of this game and classify each equilibrium as pooling, partially separating or fully separating.