Reference no: EM131003814
PART A:
Question 1:
a. Data on the rates of return for two different stocks, were collected over a fifty year period. The rate of return is defined as, the increase in value of the portfolio (including any dividends or other distributions) during the year, divided by its value at the beginning of the year. The rate of return is recorded as a percentage and can be either positive or negative.
Following are some descriptive statistics, prepared in MS Excel, on these rates of return. Use this information to answer parts i. - iii.
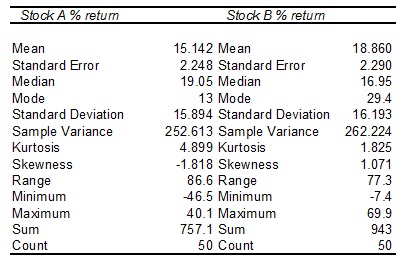
Assume that the history of stocks A and B is a useful guide to what may be expected of them in the future.
i. If you were to invest in the stock with the highest average return, which stock would you choose and why?
ii. If you were to invest in the stock with the least risk, which stock would you choose and why?
iii. Is the shape of the distribution of returns for stock A skewed or symmetric. If skewed include the direction of skewness. List three indicators from the descriptive statistics provided above to justify your decision.
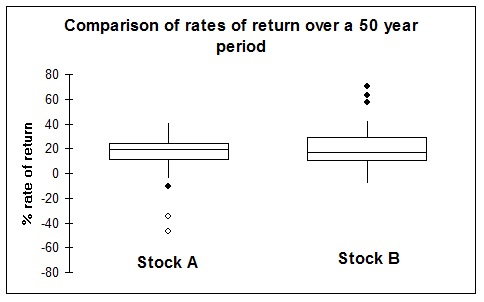
Following is a frequency distribution prepared in MS Excel, showing the distribution of the rates of return for stock B.

iv. Use this frequency distribution to construct a histogram to display these rates.
Following is an ogive comparing the rates of return for stocks A and B.
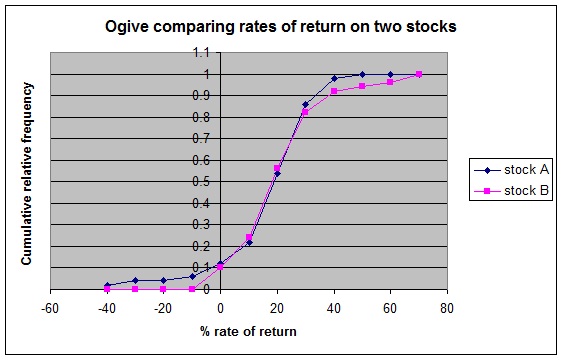
v. Use the ogive to estimate the number of years in which the average rate of return for stock A exceeded 30%.
b. Grace Bros recently advertised a sale on ladies clothing. Fifty customers were randomly selected and the amount spent at the sale was recorded. These amounts are summarised below.
Amount spent ($) No. customers
> 0 up to and including 50 3
> 50 up to and including 100 6
> 100 up to and including 150 7
> 150 up to and including 200 11
> 200 up to and including 250 15
> 250 up to and including 300 8
Total 50
i. Use the statistics functions on your calculator to estimate the mean and standard deviation amount spent by the fifty customers.
ii. Your answers to part i. are only estimates. Explain why.
Question 2:
a. Surveys of teenage girls have shown that 35% are smokers and 45% are drinkers (consume alcohol on a regular basis). Does it necessarily follow that 80% of teenage girls are either smokers or drinkers? Explain.
b. The amount of petrol, which an estate agent used in driving prospective buyers around the city to inspect home units, was recorded each week for 200 weeks. The amounts were found to follow an approximate normal distribution with a mean of 75 litres and standard deviation of 12 litres.
i. Find the probability the fuel consumption was more than 70 litres.
ii. Find the probability the fuel consumption was less than 60 litres.
iii. Estimate the number of weeks the fuel consumption was less than 60 litres.
iv. What fuel consumption was exceeded in only 20 out of the 200 weeks?
c. Leakage from underground petrol tanks at service stations can damage the environment. It is estimated that 25% of these tanks leak. 15 tanks are chosen at random, independently of each other, and examined.
i. What is the expected number of leaking tanks?
ii. What is the probability that 10 or more of the 15 tanks leak?
iii. What is the probability that fewer that three leak?
Question 3:
a. A financial controller is interested in the number of defective items produced each hour by a machine in the factory. A random sample of 25 hours produced the following number of defectives per hour.
10 6 5 7 8 4 5 5 6 8
4 3 7 8 4 10 5 3 2 0
5 8 9 3 7
i. Find a point estimate of the population mean number of defectives that the machine produces per hour.
ii. Find the standard error of the estimate in i.
iii. If we assume that the number of defectives in the population follows a normal distribution, construct a 95% confidence interval estimate for the mean number of defectives that the machine produces per hour.
iv. If you were told that the population standard deviation of the number of defectives that the machine produced per hour was 1.80, would it change your answer to part iii.? If so, find the new answer. If not, explain why.
b. A fast food franchiser is considering building a restaurant at a certain location. According to a financial analysis, a site is suitable only if the number of pedestrians passing the location averages more than 100 per hour. A random sample of 50 hours produced a mean of 110 pedestrians and a standard deviation of 12 pedestrians per hour.
i. Do these data provide sufficient evidence to establish that the site is acceptable? (Use α = 0.05)
ii. What is the consequence of Type I error here?
iii. Considering your answer to part ii., should you select α to be large or small? Explain
Question 4:
a. A homebuilder's association lobbying for various home subsidy programs argued that, during periods of high interest rates, the number of building permits issued decreased drastically, which in turn reduced the availability of new housing. Data relating housing loan interest rates (%) and the number of building approvals in thousands, were collected. The data appear below.
Year Interest rates (%) (housing loans) Building approvals (000s)
1969 7.50 155.9
1970 8.25 141.8
1971 8.25 151.3
1972 7.75 188.4
1973 7.75 179.7
1974 9.50 121.3
1975 11.50 146.1
1976 10.50 141.4
1977 10.50 123.8
1978 10.50 127.5
1979 10.50 145.3
1980 10.50 156.5
1981 11.50 138.5
1982 13.50 116.4
1983 12.50 150.8
1984 11.50 160.5
1985 12.00 140.7
1986 15.50 120.8
1987 13.50 151.2
1988 17.00 186.4
1989 16.50 141.9
1990 13.00 127.4
1991 10.50 151.5
1992 9.50 172.3
1993 8.75 188.8
1994 10.50 171.1
1995 9.75 124.7
1996 7.20 136.6
1997 6.70 156.5
MS Excel was then used to generate the following scatterplot.
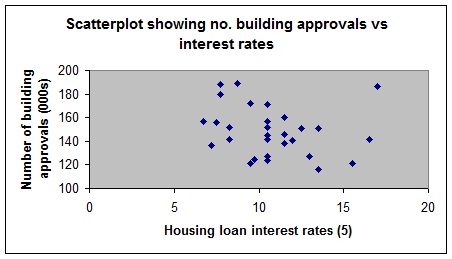
i. From the scatterplot, does it appear that the home builder's association argument is true, ie does it appear that the number of building permits decreased drastically during periods of high interest rates? Explain.
ii. There appears to be one obvious outlier in the scatterplot. In which year does the outlier occur?
iii. It appears this outlier is a data entry error. Explain why seems the most logical conclusion and how we could best fix the error before fitting the regression.
After fixing the error, MS Excel is used to fit a simple linear regression to the data and the output produced by Excel follows.
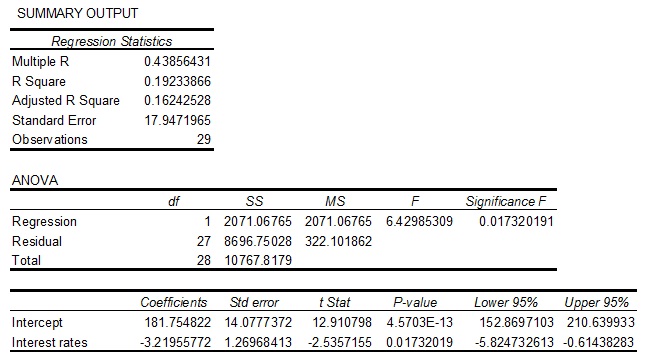
iv. Use the output provided to determine the correlation coefficient relating interest rates and number of building permits issued. Interpret this value.
v. Use the output provided to determine whether a significant linear correlation exists between interest rates and number of building permits offered. Use a 1% significance level.
vi. If the test in part v. was repeated using a level of significance of 5%, would this change your conclusion? If yes, how and why would the conclusion change. If not, why not.
b. For a test market, find the sample size needed to estimate the true proportion of customers satisfied with a certain new product to within ±0.01 at the 95 percent confidence level. Assume you have no information about the value of the proportion.
PART B:
1. Which of the following is an example of a population parameter?
A. x‾
B. n
C. μ
D. s
E. all of the above
2. When a distribution is symmetrical and has one mode, the highest point on the curve is referred to as the
A. range.
B. mode
C. median
D. mean
E. mode, median and mean, but not the range.
3. For a skewed distribution, the best measure of central tendency to report
A. is the mean.
B. is the median.
C. is the range.
D. depends on the direction of skewness
E. is the mode.
4. The actual number of cups, which can be made from a sample of 20 different brands of coffee makers, is given below.
11.0 10.5 9.0 11.0 8.5 8.5 8.5 10.5 9.5 9.0
11.5 10.5 11.0 9.0 9.5 11.0 9.5 11.0 9.0 10.5
The median number of cups from these coffee makers is
A. 9.0
B. 9.5
C. 9.75
D. 10.0
E. 10.5
5. In a grouped frequency distribution the class intervals should be mutually exclusive. This means that they should be
A. of the same length.
B. open ended.
C. not open-ended.
D. not overlapping.
E. none of the above.
6. The random variable "the number of STD phone calls made per month" is
A. quantitative and discrete.
B. quantitative and continuous
C. qualitative and discrete
D. qualitative and continuous
E. categorical.
7. A coin is tossed five times. The probability of obtaining only one head in five tosses is
A. 1/64
B. 1/32
C. 1/16
D. 5/16
E. 5/32
Use the following information to answer questions 8., 9. and 10.
The owner of a restaurant is interested in studying the demand by patrons for the Friday to Sunday weekend time period. Records were maintained that indicated whether a dessert was ordered and the gender of the individual. The results were as follows
Dessert ordered Male Female
Yes 96 40
No 224 240
A patron is selected at random.
8. Find the probability the patron will be male.
A. 0.3
B. 0.7
C. 0.192
D. 0.373
E. 0.533
9. Find the probability the patron orders dessert and is female.
A. 0.067
B. 0.106
C. 0.693
D. 0.627
E. 0.160
10. Find the probability the patron is a male, given he did not order dessert.
A. 0.747
B. 0.483
C. 0.373
D. 0.300
E. 0.933
Use the following information to answer questions 11. and 12.
In a clothing factory, the average number of machines that are inoperable on a given day is three. Machine breakdowns occur randomly and independently.
11. What is the probability there will be six inoperable machines on any given day?
A. 0.966
B. 0.050
C. 0.986
D. 0.028
E. 0.077
12. What is the probability there will be less than 2 inoperable machines over two days?
A. 0.199
B. 0.398
C. 0.062
D. 0.019
E. 0.017
13. Z is the standard normal random variable. Find P(Z < 1.70)
A. 0.3577
B. 0.8577
C. 0.4554
D. 0.9554
E. 0.0446
14. The length of time customers queue for service from a bank teller follows a normal distribution with μ = 3 and σ = 1 minutes. A random sample of 16 customers is chosen. The probability that the average waiting time in the queue is less than 2.5 minutes can be found using
A. P(Z < -0.5)
B. P(t < -0.5)
C. P(Z < 2)
D. P(Z < -2)
E. P(t < -2)
15. After taking a sample and calculating x‾, a statistician says, "I am 88 percent confident that the population mean is between 106 and 122. What does she really mean?
A. The probability is 0.88 that μ is between 106 and 122.
B. The probability is 0.88 that μ = 114, the midpoint of the interval.
C. 88 percent of the intervals calculated from samples of the same size will contain the population mean.
D. All of the above ie A., B. and C.
E. A. and C. only.
Use the following information to answer questions 16. and 17.
Suppose we wish to test whether a population proportion is significantly larger or smaller than 0.2. We take a sample of 100 and find pˆ = 0.15.
16. What should our alternative hypothesis be?
A. p = 0.15
B. p ≠ 0.15
C. p < 0.2
D. p ≠ 0.2
E. p = 0.2
17. The standard error of the proportion would be
A. 0.0335
B. 0.0400
C. 0.0200
D. 0.0016
E. 0.0357
Use the following information to answer questions 18., 19 and 20.
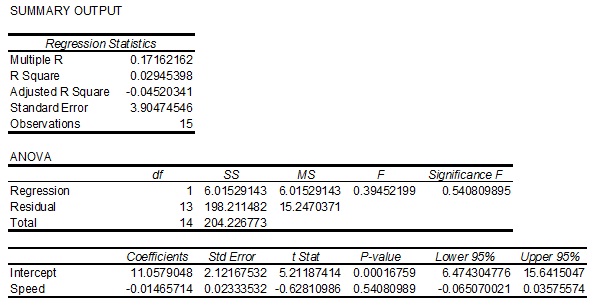
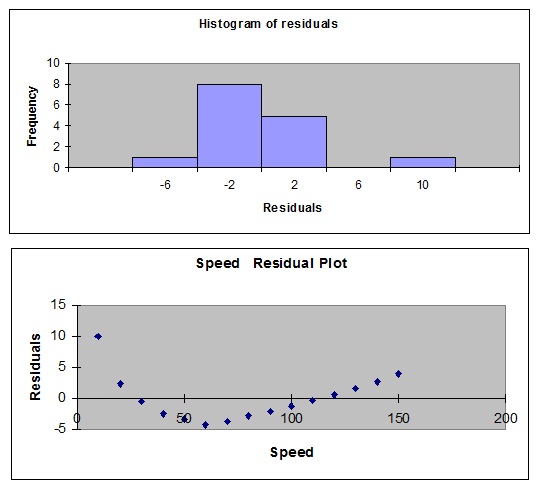
Data on the speed of a car and it's fuel consumption were collected on 15 randomly selected Ford Escorts. The manufacturer was interested in how the fuel consumption varied as the car's speed increased. A least squares regression line was fitted to the data using MS Excel. The output from this regression follows. Use this output to answer questions 18., 19 and 20.
18. The simple linear regression equation for predicting fuel consumption by using speed as an explanatory variable is given by
A. yˆ= 11.058x - 0.015
B. yˆ= 11.058 - 0.015
C. yˆ= 11.043x
D. yˆ= 11.058 - 0.015x
E. cannot be determined with out the data set.
19. The standard error of estimate is
A. 3.905
B. 2.122
C. 0.023
D. 6.016
E. unable to be determined with out the data set.
20. The two plots provided, can be used to identify violations in the assumptions of the error variable. Choose the most correct statement regarding these assumptions for this regression.
A. The residual plot indicates a linear model may be appropriate.
B. The residual plot indicates the errors have constant variance.
C. The residual plot indicates a non-linear model may be appropriate.
D. The histogram of the residuals indicates the errors are normally distributed.
E. The two plots indicate there are no violations in the assumptions of the error variable.