Reference no: EM133168398

Unit 8 Maths for Construction - Higher National Certificate Construction and the Built Environment

Assignment - Assisting with Construction Mathematical problems

Learning Outcome 1: Use analytical and computational methods to solve construction related problems

Learning Outcome 2: Investigate applications of statistical techniques to interpret, organise and present data by using appropriate computer software packages

Learning Outcome 3: Illustrate the wide-ranging uses of calculus within different construction disciplines by solving problems of differential and integral calculus

Learning Outcome 4: Use mathematical methods to solve vector analysis, arithmetic progression and dimensional analysis examples

Assignment Brief: Scenario

You have been contracted as a mathematical consultant to work with a large building development consortium. They employ a range of trades people who are constantly dealing with converting from metric to imperial and vice versa. You are also contracted to solve and confirm a number of complex mathematical problems/solutions for projects on a regular basis from the different departments within the firm. There are a range of scenarios and tasks below - work through them and present your answers in a report of four sections related to each task.

TASK 1

• You are asked to provide a pamphlet with a range of common conversions found generally in construction that can be given as a useful aide memoire to the many tradesmen (plumbers, electricians, plasterers etc, i.e. non-technical audience) employed by your company. You decide to provide a handy conversion table and twenty or so worked examples. Complete the table below and provide six worked examples for each of the following three factors: length, weight and volume.

Conversion Table

METRIC TO IMPERIAL			IMPERIAL TO METRIC
From	To	Multiply by	From	To	Multiply by
meters	yards		yards	metres
metres	feet		feet	metres
centimetres	Inches		inches	centimetres
kilometres	miles		miles	kilometres
grams	ounces		ounces	grains
kilograms	pounds		pounds	kilograms
litres	quarts		quarts	litres
litres	gallons		gallons	litres

(b) A building services engineer is to design a water tank for a project. The tank has a rectangular area of 26.5m2. With the design specifics of the width being 3.2m shorter than the length, calculate the length and width to 3 significant figures for resource requirements.

(c) You have received a letter regarding the project your company is working on. It has a penalty clause that states one of the sub-contractors working on the building for you will forfeit a certain sum of money each day for late completion. (i.e. the contractor gets paid the value of the original contract less any sum forfeit). If she is 5 days late, she receives £4250 and if she is 12 days late, she receives £2120. Calculate the daily forfeit and determine the original contract.

(d) You have been asked to investigate the following arithmetic sequences
An arithmetic sequence is given by b, 2b/3, b/3 , 0.......
• Determine the sixth term
• State the kth term
• If the 20th term has value of 15 find the value of b and the sum of the first 20 terms

(e) • For the following geometric progression 1, 1/2, 1/4 ........ determine
• The 20th term of the progression

The value of the sum when the number of terms in the sequence tends to infinity and explain why the sequence tends to this value Sn = ∑_n=0^n→∞ arⁿ

(f) Solve the following Equations for x
2Log (3x) + Log (18x) = 27
2LOG_e(3x) + LOGe(18x) = 9

(g) Given the flowing 2 by 2 matrices A and B

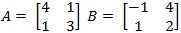
Calculate A + B, A - B, AB, A^-1, B^-1, B^-1A^-1 and (AB)^-1, A^T, B^T, (AB)^T, B^TA^T

Comment on the matrices B^-1A^-1 and (AB)^-1 and on the value of (AB)^T and B^TA^T

TASK 2
In your capacity as maths consultant to the company, you work across several departments and each department have a range of mathematical queries that they wish you to investigate for them. Using appropriate computer software packages, interpret, organise and present relevant data in answer to the following queries.

From the finance department. The finance director comes to you to ask for some assistance in presenting some revenue figures. You are asked to investigate the following data for the company.

Revenue	Number of customers
	January	June
Less than 5	27	22
5 and less than 10	38	39
10 and less than 15	40	69
15 and less than 20	22	41
20 and less than 30	13	20
30 and less than 40	4	4

(a)

• Produce a histogram for each of the distributions scaled such that the area of each rectangle represents frequency density and find the mode.
• Produce a cumulative frequency curve for each of the distributions and find the median, and interquartile range.
• For each distribution find the:
• the mean
• the range
• the standard deviation
(b)
• From procurement, they have a query about light bulbs:

At present the firm is using type A light bulbs which have a lifetime which is normally distributed with mean 360 days and standard deviation of 60 days. At present there are 5000 bulbs in a large building and they are all changed at 282 days
(i) How could the assumption that the bulb life is normally distributed be tested?
(ii) What is the probability that a single light bulb fails before 282 days?
(iii) What practical considerations might dictate such a replacement policy?
(iv) A single room has 10 light bulbs. What is the probability that more than one bulb has
failed after 282 days? (Hint use binomial distribution)
(v) What is the approximate probability that more than 10% of the 5000 total light bulbs have failed after 282 days, when they are all changed? (Hint use normal approximation of binomial distribution)
(vi) Type B bulbs which have a lifetime which is normally distributed at 432 days with a standard deviation of 45 days.
(a) At what time would you change these bulbs such that the probability of failure is the same at the probability of failure of type A bulbs at 282 days?
(b) If bulb B costs 25% more than bulb A, which is more economic to use all other factors being equal?

(c)
• From the human resource section of the company:
• They have been looking at the average age of people employed by the company. A simple random sample of 10 people from the employment pool has a mean age of 27 years. Can we conclude that the mean age of all the people employed by the company is not 30 years? The variance of the ages of those employed is known to be 20. Test your chosen hypothesis at a 5% level of significance using both a two tailed test and a one tailed test and explain your conclusions.

TASK 3
You are approached by a team from the company who are working on a project to develop a new school and have the following queries.

(a)
• The bending moment, M of a beam is given by
M = 3000 - 550x -20 x²
• Plot the bending moment and determine where the bending moment is zero
• Investigate and state the range of values where the above Bending Moment Function ls maximum or Minimum, decreasing or increasing or neither.

(b)
• The temperature θ°C at time t(mins) of a body is given by
θ = 300 +100e^-0.1t
• Evaluate θ for t = 0, 1, 2 and 5
• Determine the range of the temperature for positive t
• Determine the rate of change of the temperature at time 2. (Hint find dθ/dt)

(c)
• The cost of manufacture for a particular component, £C, is related to the production time (t)minutes, by the following formula
C=16t^-2+2t
• Investigate the variation of cost over a range of production times from 1 minute to 8 minutes
• Plot the cost function over the given range
• Explain how calculus may be used to find an analytical solution to this problem of optimisation.
• Use calculus to find the production time at which the cost is at a turning point.
• Show that the turning point is a mathematical minimum.
• Discuss whether there would still be a minimum cost of production.

(d)
• Differentiate the function f(x) = 3sin(2x) + 5log_e(x)
• Differentiate the function g(x) = e^cos(x) (Hint use function of a function differentiation)

(e)
• A table top is to be made in the shape of the area between the x axis, the line x = 1.5 and the quadratic y = x2.
• Calculate the area of the table top. (Hint use polynomial integration)

 

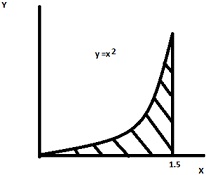
(f) Integrate the following

(i) ∫3/x dx

(ii) ∫Sin3θ dθ

(g) An asymmetric heat conductor within a building is such that the differential of the rate of heat transfer with respect to temperature difference T is e0.03T. T is the difference between the outside and inside temperatures in degrees Celsius That is

dP/dT=e^0.03T

Given that P = 0 when T = 0, determine P as a function of T and plot the function P(T) for values of T ranging from- 20 degrees to + 20 degrees (Hint use integration)

TASK 4

a) One of the design engineers working for the company come with the following information and queries. A support beam, within an industrial building, is subjected to vibrations along its length; emanating from two machines situated at opposite ends of the beam. The displacement caused by the vibrations can be modelled by the following equations.
x1 = 3.75 sin (100Πt + 2Π/9)
x2 = 4.42 sin (100Πt - 2Π/5)
• State the amplitude, phase, frequency and periodic time of each of these waves.
• When both machines are switched on, how many seconds does it take for each machine to produce its maximum displacement?
• At what time does each vibration first reach a displacement of -2mm?
• Using appropriate spreadsheet software, copy and complete the following table of values:

t	0.000	0.002	0.004	0.006	0.008	0.010	0.012	0.014	0.016	0.018	0.020
x1
x2

• Plot the graphs of x1 and x2 on the same axes using any suitable computer package or otherwise.
• Extend your table to include x1 + x2 and plot this graph on the same axes as the previous two
• State the amplitude and frequency of the new wave.

b) A pipeline is to be fitted under a road and can be represented on 3D Cartesian axes as below, with the x- axis pointing East, the y-axis North, and the z--axis vertical. The pipeline is to consist of a straight section AB directly under the road, and another straight section BC connected to the first. All lengths are in metres.

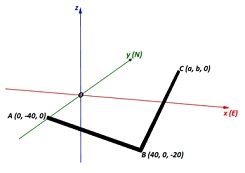
• Calculate the distance AB.
• The section BC is to be drilled in the direction of the vector 3i + 4j + k.
• Find the angle between the sections AB and BC.
The section of pipe reaches ground level at the point (a, b, 0).
• Write down a vector equation of the line BC. Hence find a and b.