Reference no: EM132410980
Assignment - Monte Carlo Methods with Financial Applications
The assignment consists of four problems. The objective of the first problem is to test the understanding of some mathematical fundamentals of Monte Carlo simulations. The remaining problems are concerned with option pricing. The options featuring in these problems should be priced in two ways: first, with the help of a direct Monte-Carlo simulation, and then again with Monte Carlo simulation using two different variance reduction techniques (one for each problem). In problem 2 you should use importance sampling but in problems 3 and 4 you may choose yourself which variance reduction techniques to use.
Each solution should include a careful analysis of the results. The quality of both the numerical simulation and the analysis will be decisive in determining the final grade. Both the code, which can be done in computing environment of your choice, and the underlying mathematical reasoning should be clearly presented with detailed comments and arguments.
Tasks - The statements of the problems
1. Let K denote the regular octagon with the vertices
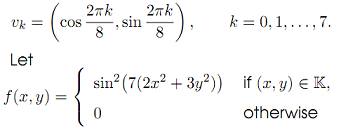
(a) Generate 3000 uniformly distributed points in K and plot the outcome.
(b) Using the acceptance-rejection method generate 3000 points in K which are distributed according to the probability density function of the form f /C, where C > 0 is a normalizing constant, but without calculating the value of C. Plot the outcome.
IMPORTANT: In the option pricing problems below, it is assumed that we are working within the standard risk neutral setting with a constant risk-free rate and the geometric Brownian motion used to model stock prices. For all estimates form approximate confidence intervals (=empirical confidence intervals) at the 95% level of confidence and calculate the approximate relative error (=empirical relative error).
2. Assume that r = 1.9% is the risk-free rate. Consider a range of European call options expiring in 6 months, with different strike prices, all written on the same stock. The price process S(t) of this stock is modeled by a Geometric Brownian Motion with the initial price S(0) = 100 and volatility σ = 25%. Let C(K) denote the price of such an option at time t = 0, expressed as a function of the strike price K > 0. Calculate C(K) for K = 100, 125, 150, 175, 200, 225, 250 using the Black-Scholes formula. Estimate C(K), for the same range of values of K, first using a crude Monte-Carlo approach and then using importance sampling. Explain if there is any advantage of using importance sampling over crude estimates.
3. Let r = 3% be the risk-free rate. Let the prices S1(t) and S2(t) of two stocks evolve according to the geometric Brownian motions with the initial values S1(0) = 75, S2(0) = 50 and the volatilities σ1 = 30% and σ2 = 20%, respectively. Consider the Asian call option with strike price K = 65 expiring in 8 months, written over a simple portfolio of the two stocks given by the formula S(t) = 0.55 S1(t) + 0.45 S2(t). Let ρ denote the correlation coefficient between the Brownian motions W1(t), W2(t) driving S1(t) and S2(t) respectively. First, estimate the price of this option assuming that ρ = 0. Then investigate how changing the value of % to ±0.3, ±0.6, ±0.9 changes the price of this option. You may assume that there are 80 uniformly spaced monitoring dates and that the arithmetic averages are used.
4. Suppose that the risk-free interest rate is r = 2.5%. Consider a stock with the price process S(t) modeled by a geometric Brownian motion with volatility σ = 30%. The stock is assumed to be worth S(0) = 300 at present. Suppose that C(t) denotes the price at time t of the European call option written on this stock expiring in half a year, with strike price L = 300. Estimate the price of the compound put-on-call option with strike price K = 19 and maturing in 3 months, written over that call option. By considering several different values of L below and above 300, investigate how L influences the price of the compound option.
Attachment:- Assignment File.rar