Reference no: EM13726
1. Let A = {1; 2; 3; : : : ; n}.
(a) How many relations on A are both symmetric and antisymmetric?
(b) If R is a relation on A that is antisymmetric, what is the maximum number of ordered pairs that can be in R?
(c) How many antisymmetric relations on A have the maximum size that you determined in part (b)?
2. Consider the relation on A = {1; 2; 3; 4} with relation matrix:
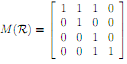
Assume that the rows and columns of the matrix refer to the elements of A in the order 1; 2; 3; 4.
(a) Draw the digraph for the given partial order.
(b) Draw the Hasse Diagram for the partial order.
(c) How many total orders contain the given partial order as a subset?
3. Let R and S be relations on a set A. For each of the following statements, determine whether it is true or false. In each case, provide a proof or a counterexample, whichever applies.
(a) If R and S are transitive, then R ∪ S is also a transitive relation on A.
(b) If R is symmetric and transitive, then R is also re exive.
(c) If R and S are partial orders on A, then R ∩ S is also a partial order on A.
4. Let S be the set of all nonzero real numbers. That is, S = R {0g. Consider the relation R on S given by xRy i� xy > 0.
(a) Prove that R is an equivalence relation on S, and describe the distinct equivalence classes of R.
(b) Why is the relation R2 on S given by xR2y i� xy < 0 NOT an equivalence relation?
5. For a function f : Z → Z, let R be the relation on Z given by xRy i� f(x) = f(y).
(a) Prove that R is an equivalence relation on Z.
(b) If for every x ε Z, the equivalence class of x, [x], contains exactly one element, what can be said about the function f?
(c) If f is the function de�ned by f(x) = x2 , describe the equivalence classes of R.