Reference no: EM132315285

Manufacturing, Control and Environmental Sustainability - Control design for a conveyor system Assignment

Learning outcomes - The learning outcome of this assessment is for the student to: Critically analyse the effectiveness of a feedback control system for a practical engineering application.

This project is uses MATLAB/SIMULINK and the Control System Toolbox in order to design a Proportional/Integral controller for a Conveyor system.

Deliverables - The following deliverables must be submitted by the project deadline:

1. Open loop transfer function model of the conveyor system.

2. Your MATLAB code that designs your proposed controller (appendix to the project report).

3. Transient response plots of the designed control system.

4. A project report explaining:

a. How you derived the open loop transfer function of the conveyor system.

b. How you designed and tuned the controllers and the reasoning behind your design choices.

c. A comparison between the controllers designed.

Manufacturing system (Conveyor system) -

Manufacturing systems often include conveyor belt systems. This will require the use of some form of motor to actuate the process. The measurements will vary depending on the process variable to be controlled. Generally, conveyor systems may use a belt on rollers to transport products. The rollers are driven by motors. The velocity of the conveyor is generally held constant to optimize the process. The speed of the conveyor belt may be measured using an optical encoding system. The first important task is to be able to evaluate what the inputs and outputs of any particular system are and subsequently be able to produce a differential equation model to represent every element in the system.

Task 1 - Modelling the Conveyor System

a) Assuming zero initial conditions, find the Laplace transforms of the differential equations derived above for the following

(i) The conveyor

(ii) Transducer (Incremental Rotary Encoder)

(iii) The DC motor

b) Using the results in a), show that the transfer function for the following

(i) The conveyor G(s) = 1/(Js + B'), where ω^-(s) = G(s)τ^-(s)

(ii) The transducer G_m(s) = 159.155, where ω^-_m(s) = Gm(s)ω^-(s)

(iii) The DC motor G_d(s) = K_m/(L_as+R_a), where τ^-(s) = G_d(s)(v^-_a(s) - v^-_b(s)),

c) Construct a block diagram outlining all the signals and the transfer functions derived in b).

d) Simplify the block diagram in c) to evaluate a transfer function between the input signal v^-_a(s) and the output signal ω^-(s).

e) Calculate the undamped natural frequency ω_n, the damping ratio ζ and the steady state gain G(0) = K.

f) Verify that the model is open-loop stable by graphically computing the poles of the open loop system.

g) Using inverse Laplace transforms, and assuming that input signal v^-_a(s) is a unit step signal, evaluate the step response of the conveyor velocity ω(t).

h) Using MATLAB, produce an open-loop unit step response for the output of the conveyor and verify the result by comparing it with the analytical result derived in g). Select the time scales so that both the transients and the steady state output are visible.

Task 2 - Controller design in MATLAB/SIMULINK

For this task, it is required to use the open loop transfer function obtained from (Task 1) to design a PI controller using a feedback loop arrangement described for the following signals and systems.

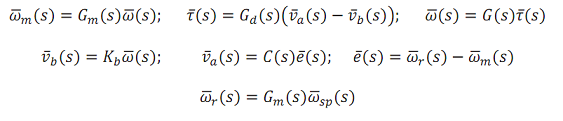
a) Construct a block diagram depicting the feedback loop arrangement for the signals and transfer functions defined above.

b) Calculate the values of K_p and K_i using the heuristic approach.

c) Analytically, derive the following:

(i) The transfer function from reference signal ω^-_r(s) to the error e^-(s).

(ii) The transfer function from reference signal ω^-_r(s) to the controller output v^-_a(s).

(iii) The transfer function from reference signal ω^-_r(s) to the conveyor output ω^-(s).

d) Analytically calculate the following:

(i) The steady state error e_ss.

(ii) The closed loop steady state output of the conveyor ω_ss.

(iii) The closed loop steady state output of the controller v_{f_ss}.

e) For this task, different values of the un-damped natural frequency (ω_n) and damping ratio (0 < ζ ≤ 1) will be given to you and this will be announced by the tutor in accordance to the table outlined in the "Controller Specification" section.

(i) Using MATLAB, design your K_p and K_i parameters of the PI controller to meet the design requirements outlined in tables 1&2. Confirm using MATLAB that the required natural frequency ω_n and damping ratio ζ of the closed loop transfer function between r^-(s) and ω^-(s) is met.

(ii) What is the resultant characteristic equation of the following closed-loop system? What are the poles and zero locations of the closed loop system? Comment on the transient behaviour using second order performance specifications (i.e. Maximum overshoot, settling time, etc.)

Task 3 - Project Report

Write a project report on the analysis and design of the closed-loop system outlining a comparison between the two controllers designed in task 2. You need to justify the reasoning behind the choice of the PI controller parameters and how they have met the criteria for the transient response design specifications outlined. You may investigate this from a stability and performance point of view (i.e. using MATLAB tools such as PZMAP, STEP) and the resultant performance specification (i.e. peak time, overshoot, settling time, etc.).

You need to ensure the following:

• Demonstrate your results with suitable MATLAB/SIMULINK plots & code (very, very strict rule).
• All m-files and SIMULINK block diagrams must be included in the appendix section of your report (very, very strict rule).
• Label the axes of each graph. This includes attaching a figure legend when appropriate. Include the unit with the label itself ("speed m/s" versus "time in milliseconds" or "time [ms]") so that we know what's being measured and that it is not an arbitrary variable (very, very strict rule).
• Instead of sending many figures for one question, you can use the subplot command to group relevant figures (not-so-strict rule).
• Every m-file code must contain some comments describing the function of the MATLAB code/command (very, very strict rule).
• Every graph must have a descriptive Title. Label and Scale All axes (very, very strict rule).
• If a plot contains multiple lines, you must add a legend explaining each curve. (very, very strict rule).
• For SIMULINK *.mdl block diagrams, avoid overlapping and crossing lines as much as possible. Re-arrange the icons so that a clear path from left to right is visible. (very, very strict rule).
• Number plots and graphs sequentially, e.g. Fig.1, 2 etc. (very, very strict rule).

Attachment:- Assignment Files.rar