Reference no: EM13342845

Question 1. Let n and r be non-negative integers. Prove that

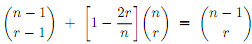
Question 2.

(a) Let A be a non-empty set, and Ρ an equivalence relation on A. Let a, b 2 A. Prove that [a] = [b] ↔ a Ρ b.

(b) If Ρ is both an equivalence relation and (simultaneously) a partial order on A, describe Ρ.

Question 3. For each relation Ρ described below, determine if Ρ is reflexive, symmetric, transitive, anti-symmetric. In each case, if Ρ is an equivalence relation, describe the equivalence classes.

(a) A = R, and aΡ b if and only if sin a = sin b.

(b) A = Z, and aΡ b if and only if 5 j (2a + 3b).

(c) A = Z x Z, and (a; b)Ρ (c; d) if and only if a + b ≥ c + d.

(d) A = P(Z) (the power set of Z). Let X ⊆ Z be a fixed set. Define Ρ on A by B Ρ C if and only if B ∩ X = C ∩ X.

(e) Two sequences of real numbers (an) and (bn) are eventually equal if there exists some K  ∈ Z such that a_k = b_k for all k ≥ K. Let A be the set of all sequences of real numbers, and define Ρ by (an)Ρ(bn) if and only if (an) and (bn) are eventually equal.

Question 4. If Ρ is a relation on a set A, define Ρ² by a²Ρb if and only if there exists c with a Ρc and c Ρ b. If Ρ is reflexive/symmetric/transitive does Ρ² have the same property?