Reference no: EM13374900

Amalia, Alexia, and Ariane work together in a homework group on a problem set. Each group member i = 1,2,3 can exert effort ?e_i(0 ≤ e_i ≤ 1) on the problem set at . Their grade for the problem set G depends on the sum of their efforts in the following way:

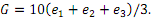
The utility for group member ?is given by U_t = G - C(e_i).

a) Suppose Amalia, Alexia, and Ariane choose their effort independently. How much effort do they exert in the Nash equilibrium?

Amalia is not satisfied with the result of the first problem set. She decides to bake a cake and use that as an incentive device to motivate her group members to do a better job on the next problem set. As effort is not perfectly observable, the three students decide to make each of them responsible for 1/3 of the problem set. The student obtaining the highest number of points for her part of the problem set wins the cake. More in particular, for group member ?, the probability of winning the cake equals

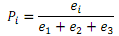
Now, suppose that each group member assigns value v to the cake and that all maximize their expected utility: U_t = G + P_iv - C(e_i)

b) How much effort do the students exert in the Nash equilibrium of the game introduced by Amalia?

c) What value for the cake induces the students to exert the efficient effort level?

Now, suppose that the three students repeatedly do homework in the same group. Amalia is tired of making cakes all the time. Alexia suggests the following: "Why don't we just all expend the efficient level of effort? If one of us deviates by exerting less effort, we can punish her by choosing the Nash equilibrium effort under a)."

d) Derive the trigger strategy stability condition for the strategy suggested by Alexia.