Reference no: EM13181214

An Alternative Interpretation of Ricardian Equivalence?

The government and the representative consumer each live for both periods of the economy, and suppose there are never any credit constraints on the consumer. The government does not have access to lump-sum taxes, only proportional consumption taxes. However (this is different from our baseline framework), the consumption taxes the government collects in a given period are not restricted to be levied on consumption from only in that period.

To be more precise, suppose that total consumption tax revenues the government collects in period 1 are based only on period-1 consumption (because there was no period zero, say). However, total consumption tax revenues the government collects in period 2 are based on both period-1 consumption and period-2 consumption. That is, a portion of the revenue collected in period 2 is based on period-1 consumption, and the remaining portion of the revenue collected in period 2 is based on period-2 consumption.

Denote by pia the tax rate on period-1 consumption that is levied in period 1: denote by viz the tax rate on period-1 consumption that is levied in period 2: and by r22 the tax rate on period-2 consumption that is levied in period 2. There is no r23 (which would represent the tax rate on period-2 consumption that is levied in period 3) because the economy does not exist in period 3.

With this notation, the government's period-1 and period-2 budget constraints in real terms are:

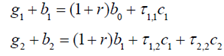
The representative consumer's period-1 and period-2 budget constraints in real terms are:

 

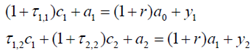
For simplicity, suppose the government and consumers each begin period 1 with zero assets. As usual, you can think of all the tax rates as being numbers between zero and one (but they need not be so restricted). The remainder of the notation is as in class.