Reference no: EM131466900

Part 1 - Civil Engineering Numerical Analysis

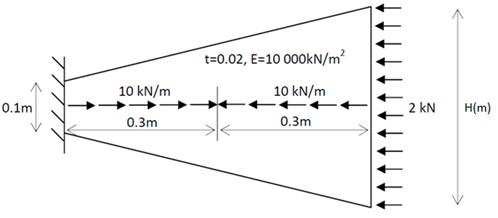
H(m) = 0.3(m).

1. Treating the bar illustrated above as being a one dimensional axial bar where plane sections remain plane and parallel, analyse the bar using the Galerkin finite element method. The coding solution for linear h-refinement and its manual solution for a limited number of linear elements areon Blackboard for your reference.

Consider h-refinement using three-noded quadraticelements, produce the manual solution for when the domain includes of 2 equal spacing quadratic elements. Generate the outcomes to produce:
a. Nodal displacements
b. Displacement at the left quarter of each element.
c. Normal stress at the left quarter of each element.

2. The bar illustrated above is solved as a two dimensional plane stress problem. This task allows you to start with FEM programming at very beginning level. You will be given full coding solution and asked to extract a number of results given by running the problem FEM program.

Modify the code to yield 2 equal spacing 4-noded quadrilateral elements along x-axis. Generate the outcomes to produce:
a. Each element coding loop: indexArray, K, f.
b. Global K, f, u.
c. Nodal stresses.

3. Extend the two-noded linear Matlab program provided to produce the corresponding solution for three-noded quadratic elements. You need to amend all sub function m-files, and the main m-file. Debug your code to confirm if it works properly before put all files in a zip folder for USB submission.

Hints:

1. Time management: Questions 1 focuses on detailed calculation for FEM understanding. Questions 2 and 3 practises you lightly for programming FEM using Matlab and further strengthening your understanding for FEM. With multiple members in group, you can consider to start on all questions at once and do them concurrently. All 3 questions are independent from each other. Assign the work share efficiently among your group to take good use of the number of members.

2. Approach and result confirmation: Question 1 is an upgrade of the solution that we fully detailed for linear elements in class, you are advised to follow closely solution steps for linear elements to generate the solution for quadratic elements. For Question 2, the solution derivation in Matlab coding is already on Blackboard. Have a good study to understand and generate the pairing manual calculation outcomes.