Reference no: EM13371493
A Computational Study of a Spring-Mass System in Steady State
Idealized spring-mass systems have numerous applications throughout engineering. Fig.1 shows an arrangement of three masses and four springs which, after is released, is pulled downward by the force of gravity. The springs are made of the same homogeneous, isotropic, linear elastic solid material. This means that the springs are identical and follow Hooke's law (the strain-stress constitutive curve is a straight line of slope K > 0). The system of ordinary differential equations satisfied by this system follows from Newton's second law of motion:
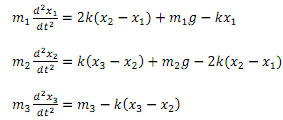
where g is the gravitational acceleration, m1, m2, m3 are the masses, K > 0 is the spring constant of elasticity (also known as the Young's modulus), and x1, x2, x3 are the displacements of the masses.
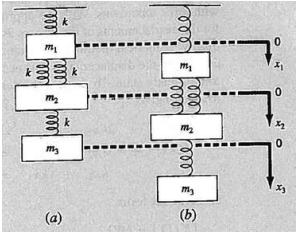
At equilibrium, when the system finally reaches its steady state, the above system of equations (1)-(3) becomes a system of linear algebraic equations of the form:
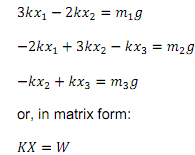
where K , called the stiffness matrix, is:
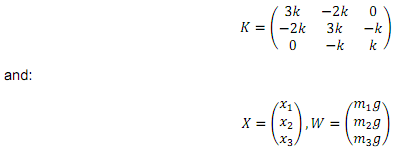
are the column vectors of the unknown displacements X and the weights W, respectively.
1. Using equations (1)-(3) and Fig.1, name the forces acting on each of the three masses.
Let m1= 2 Kg, m2= 1 Kg, m3= 1 Kg, k = 10 m/s2 and = 2 Kg/s2 and solve system (7) using:
2. Cramer's rule;
3. The LU decomposition with Gauss elimination;
4. The inverse of the stiffness matrix (calculated using the LU decomposition with Gauss elimination).
What is the physical interpretation of the elements of ? Write C++ programs for steps 2, 3, and 4. Present the pseudo-codes for steps 2, 3, and 4. Compare the results obtained using these three methods and comment on which method performs better.