Reference no: EM133043745

2010ODL-N Further Maths - Teesside University

Assignment 1:

Question 1. Convert the following into the number systems specified:

(a) 1101111011001₂ to octal and hexadecimal forms.

(b) 3B4E5₁₆ to denary and binary forms.

Question 2. Add the binary numbers, working in binary. Express the answer as an 8-bit number, clearly showing any carry bits.

11011110₂ + 01101101₂

Question 3. Follow the scenario and instructions clearly, and state the values as an exact value, or, correct to 2 decimal places accuracy:

(a) Given 2 complex numbers Z₁, Z₂ as:

Z₁ = 4 - 5j, Z₂ = -2 - 3j

Find: Z = 3Z₁ + 2Z₂ in Cartesian form a + b_j.

(b) The current I in an a.c. circuit is given by I = j(0.5 - 2j)/7+5j

Find the current I in polar form r∠θ.

Question 4. Convert z = -2 + j to polar form and find z⁸ using De Moivre's theorem. Plot z and z⁸ on an Argand diagram.

Question 5. The total impedance of two impedances connected in parallel is given by

1/Z = 1/Z₁ + 1/Z₂

where Z is the total impedance and Z₁ = 4 + 2j and Z₂ = 2 - 3j are the branch impedances.

Determine the current and its phase angle relative to a 110V supply voltage.

Question 6. Perform the matrix operations based on the given matrices:

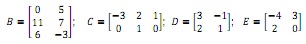
(a) B^T + C

(b) 3E - 2D^T

Question 7. Given the matrix A =

(a) Find the inverse of the matrix A clearly showing all the steps leading to the inverse matrix.

(b) Show clearly using matrix multiplication that AA^-1 = I and A^-1A = I, where I is the identity matrix.

8. The system of currents i₁, i₂ and i₃ in a circuit satisfy these equations:
i₁ + i₂ + i₃ = 0
6i₁ - i₃ = 24
7i₂ - 2i₃ = 9

Solve the system using:

(a) Matrix inversion

(b) Gaussian elimination

Give the answers correct to 3 decimal places accuracy.

Assignment 2

Question 1. The output response, f(t) of a feedback control system is given by:

f(t) = k/1+k [1 - e^-(1+k)t], where k is a constant.

Determine:

a) The value of f(3), taking k = 5. Give your answer accurate to 2d.p.

b) The inverse function f^-1(t), where k is a constant.

Question 2. The functions g and h are defined by:

g(x) = 6/3 - x; x ≠ 3

h(x) = 5x + 2

Determine:

(a) The function g(h(x).

(b) The function h(g(x)).

Question 3. Solve the equations correct to 2 decimal places accuracy.

(a) Estimate using the bisection method, the positive real root of:

ln(x⁴) = 0.7

Take the initial guess as x_L = 0.5, x_IJ = 2

(b) Estimate using Newton Raphson method, one root of:

2x³ - 11. 7x² + 17. 7x - 5 = 0

Take the initial guess as x₀ = 3.

Question 4. Evaluate ₀∫^Π/3 √sin (x) dx correct to 3 decimal places using n= 6 equal intervals, applying:

(a) Trapezoidal rule

(b) Mid-ordinate rule

(c) Simpsons rule

Question 5. Determine the general solution of the differential equations. Write out the solution y explicitly as a function of x.

(a) 3x²y² dy/dx = 2x - 1

(b) 2dy/dx + 3y = e^-2x - 5

Question 6. Determine the particular solution of the equation:

d²y/dx² + 3dy/dx + 2y = 10cos(2x) satisfying the initial conditions y(0) = 1, y′(0) = 0.

Question 7. Find the inverse Laplace transform of:

(a) 3-2s/s²-4s+9

(b) s+2/(s²+9)(s-2)

Question 8. Solve using the Laplace transform method:

d²y/dt² - 2 dy/dt + y = 5e^t and y(0) = 1, y'(0) = 1