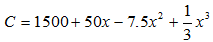Reference no: EM13374644
1. Suppose a local food retailer firm has the following cost function that depends on the daily sales of two goods: soft pretzels (z) and soft drinks (d).
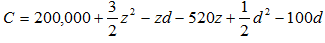
Calculate the optimal amount of pretzels and soft drinks that minimizes this firm's costs.
2. You run a steel fabrication plant that builds truck frames for Toyota. Suppose your monthly production function is Q = 200K -2K2 + 120L - (1/2)L2, where K stand for the number of machines you rent and L is the number of workers you hire. Each month the central office provides you with $160,000 of operating expenses and they want as many frames as you can provide.
a. If machines cost $4000 per month and workers cost $2000 per month, how many machines and how many workers will you use. (Note, you can hire fractions of machines and workers since this is a per month calculation.)
b. How many frames do you provide each month?
3. Your company makes its product out of two inputs, x and y according to the following production function:
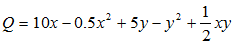
Px=$50 ;Py=$40 and your company can sell this product for $10. How much of each input should you buy, and how much money do you make?
4. You have a license with a drug company to produce a particular strain of bacteria for their laboratories (used in testing). Your licensing agreement says you must produce at least 3 million samples per year, but they will take more than that if you produce them. You are capable of producing up to 15 million. The drug company wants you to minimize your average costs, given those bounds.
If your average cost function is as shown below what level of output minimizes your average cost, and what are those costs? Note, x is measured in millions of samples per year.