1 long-run figures for the economy are reported in table

Reference no: EM13373306

1. Long-run figures for the economy are reported in TABLE 1

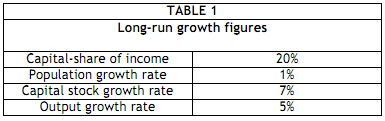
1628_compute the Solow residual.png

Assume that the country's production function is a constant-returns-to-scale Cobb-Douglas, Y = AK^aL^b, where Y is real national income, K is national capital stock and the total factor productivity is represented by A. Total population coincides with total workers and is denoted by L.

(a) compute the Solow residual

- state clearly/describe the formula you are using
- compute the mathematical result

Now consider some additional data provided reported in TABLE 2

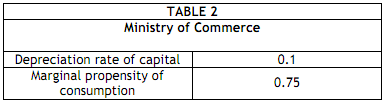
860_compute the Solow residual1.png

(b) Determine the steady state level of ‘consumption per human-capital-augmented efficiency units of labour' (c')

- state clearly/describe the formula you are using

- compute the mathematical result

- state clearly/describe the formula you are using
- compute the mathematical result

(d) Sketch graphically the representation of the steady state and illustrate what happens to the steady state when there is an increase in the rate of population growth. Explain your answer by discussing whether or not that is in line with the empirical evidence.

- state clearly/describe the graph you are using

- describe clearly the changes that occur to the graph and compare the final result with the initial situation

- give an economic intuition of the result, within the context of the model

- talk about the empirical evidence illustrated in class in relation to the effects of the exogenous change on the endogenous variables.

Reference no: EM13373306

Questions Cloud

Question 1the average household income in the us is 60000 : question 1the average household income in the us is 60000. the marginal propensity to consume mpc .90. if household

The total of the individual customer account balances : the total of the individual customer account balances should equal the balance in accounts receivable which is

Smith co bought a window franchise from paine inc on : smith co. bought a window franchise from paine inc. on january 2 2008 for 100000. a highly regarded independent

For most firms today success or failure is determined by : for most firms today success or failure is determined by the ability to find attract keep develop and tap into the most

1 long-run figures for the economy are reported in table : 1. long-run figures for the economy are reported in table 1assume that the countrys production function is a

On august 1 2010 dambro co acquired 200 1000 9 bonds at 97 : on august 1 2010 dambro co acquired 200 1000 9 bonds at 97 plus accrued interest. the bonds will be added to dambros

Garcia company began 2010 with net assets of 80000 net : garcia company began 2010 with net assets of 80000. net income calculated by using the capital maintenance concept was

The pricing objective of maximizing : the pricing objective of maximizing profitsnbspnbspnbspnbspnbspnbsp 1 has not been affected by other more socially

Question- milner frosted flakes company offers its : question- milner frosted flakes company offers its customers a pottery cereal bowl if they send in 3 box tops from

User Account

All Pages