Reference no: EM13374618

1. Let z be a T x 1 vector of random variables with joint density function f(z,θ), where θ is a k x 1 vector of unknown parameters. Derive the Cramer-Rao lower bound for the covariance matrix of an unbiased estimator of θ.

2. Consider the fixed X linear regression model:

(a) Stating clearly any conditions that you impose, derive the asymptotic distribution of the OLS estimator of β when T^-1X'X -> Q where Q is a positive definite matrix.

(b) Suppose now that X is comprised of a constant and a time trend, i.e.:

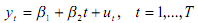
Explain why the T^-1X'X -> Q assumption is no longer appropriate. Derive the asymptotic distribution of the OLS estimator of β₂ in this framework.

3. Let x,t = 1......T, be a sample of independent and identically distributed random variables with mean E(x_t) = μ and V(x_t) = σ²

(a) State Khinchine's weak law of large numbers and provide a proof of this result.Discuss conditions under which a law of large numbers exists for a sample of independent but heterogeneously distributed random variables. Explain how these results relate to the notion of a consistent estimator of the mean μ.

(b) State the Lindeberg-Levy central limit theorem and provide a proof of this result. Explain why central limit theorems are useful in econometric analysis.

4. Let z be a T X 1 vector of independent and identically distributed random variables, with joint density function );f(z, θ), where θ is a k x 1 vector of unknown parameters.

(a) Stating clearly any assumptions that you make, prove that the maximum likelihood estimator of θ is consistent and asymptotically normally distributed. Use your result to explain why maximum likelihood estimators are asymptotically efficient.

(b) State the likelihood ratio, Wald and Lagrange multiplier test statistics for testing the null hypothesis H₀: θ = θ_o. Derive the asymptotic distributions of these three statistics under the null hypothesis.

5. Consider the fixed X linear regression model:

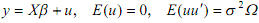
where Ω is a positive definite matrix.

(a) Prove that the GLS estimator of β is the best linear unbiased estimator for the above model. Stating clearly any conditions that you impose, show that the GLS estimator of β is consistent.

(b) Suppose the error terms are first order autocorrelated:

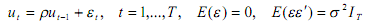
where u_o and |ρ|. Explain how to obtain a feasible GLS estimator of β, and show under suitable conditions that this estimator is consistent.