Reference no: EM13376424

1. In each case below, prove or disprove that the subgroup H is normal in the group G.

If H is normal in G, determine whether the factor group G=H is abelian.

a) Let G = GL(2,R) and le H =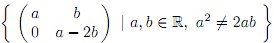

b) Let G = GL(2,R) and let H = fA 2 G j det(A) is a positive rational number g.
c) Let G = S4 and let H = h(1 4 2 3)i.
d) Let G = S5 and H = f  2 S5 j (1), (4) 2 f1, 4g g.
e) Let Φ be a homomorphism from a group G to the group Z of integers (under addition). Let H = ( a ∈ G )| Φ(a) ∈(4)}.
f) Let Φ be a homomorphism from a group G onto D5. Suppose that Φ ∈ G is such that |Φ(a)| = 2. Let H = (a).
g) Let G = A4 and let H = {e, (1 2)(3 4), (1 3)(2 4), (1 4)(2 3)

2. Let G be an abelian group of order 45. Suppose that G contains an element of order 9. Prove that G is cyclic.

3. Let r be an element of order 8 in D8 and let s be a reflection in D8. Recall that the centre Z(D8) of D8 is equal to (r⁴).
a) What is the order of the factor group D8=Z(D8)?
b) Find an element a 2 D8 such that aZ(D8) has order 4 in D8=Z(D8).
c) Prove that D8=Z(D8) is not abelian.
d) Let H = haZ(D8)i be the subgroup of D8=Z(D8) that is generated by the element aZ(D8) from part b). Prove that H is normal in D8=Z(D8).
e) Prove that any element in D8=Z(D8) that does not belong to H has order 2.

4. Let n ≥ 3 be an even integer. Let Z(Dn) be the centre of Dn.
a) Prove that the factor group Dn=Z(Dn) is nonabelian.
b) Prove that D20/Z(D20) is isomorphic to D10.

5. Let G be a nonabelian group of order 55. Prove that the centre Z(G) of G is equal to {e}.

6. Let G and G' be groups. Assume that G is nite and G0 is abelian. Suppose that Φ : G -> G' is a homomorphism and j(G)j = 12. Prove that G contains an element of order 6.

7. In each case below, prove or disprove that  is a homomorphism. If  is a homomorphism, identify the kernel of  and the image Φ(G) of Φ.

a) Let 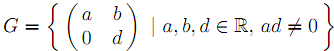, under multiplication of matrices. De fine Φ : G -> G by

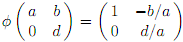
b) De fine: Z₁₀ -> Z₁₂ by

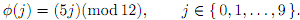
8. Let G be a group and let Φ : D9 -> G be a homomorphism. Prove that  is one-to-one.

if and only if (r3) = e for some rotation r ∈ D9.

9. Let n  3 and let r and s be elements of Dn such that jrj = n and s is a reflection. Suppose that G0 is a group and  : Dn -> G0 is a homomorphism.

a) Prove that the image (Dn) of Dn in G0 is abelian if and only if (rs) = (sr).

b) Prove that the image (Dn) of Dn in G0 is abelian if and only if (r2) = e0

10. Suppose that G1, G2 and G3 are groups,  Φ: G1 -> G2 is a homomorphism and  μ: G2 -> G3 is an isomorphism.

a) Prove that ΦKer  = Ker μ o Φ.

b) Prove that  is onto if and only if    is onto.

11. Suppose that Φ: G -> G0 is a homomorphism,  is onto and G is cyclic(resp. abelian). Prove that G0 is cyclic(resp. abelian).

12. Let  : G -> G' be a homomorphism of groups. Assume that G' is abelian. Prove that if H is a subgroup of G and Ker   H, then H is normal in G.