Reference no: EM13371631

1. Construct an explicit deformation retraction of the torus with one point deleted onto a graph consisting of two circles intersecting in a point, namely, longitude and meridian circles of the torus.

2. Construct an explicit deformation retraction of Rⁿ- {0} onto S^n-1

3. (a) Show that the composition of homotopy equivalences X→Y and Y→Z is ahomotopy equivalence X→Z . Deduce that homotopy equivalence is an equivalencerelation.

(b) Show that the relation of homotopy among maps X→Y is an equivalence relation.

(c) Show that a map homotopic to a homotopy equivalence is a homotopyequivalence.

4. A deformation retraction in the weak sense of a space X to a subspace A is ahomotopyf_t:X→X such that f₀= 11, f₁(X) ⊂A, and f_t(A) ⊂A for all t . Show that if X deformation retracts to A in this weak sense, then the inclusion mapA?Xis a homotopy equivalence.

5. Show that if a space X deformation retracts to a point x ∈X, then for each neighborhood U of x in X there exists a neighborhood V ⊂U of x such that the inclusion map V? U is nullhomotopic

6. Show that a retract of a contractible space is contractible.

7. 10. Show that a space X is contractible iff every map f :X→Y , for arbitrary Y , is nullhomotopic. Similarly, show X is contractible iff every map f: Y→X is nullhomotopic.

Group 2 :

1. Show that composition of paths satisfies the following cancellation property: If

                                                             i.      f₀.g₀?f₁.g₁ and g₀?g₁ then f₀?f₁.

2. Show that the change-of-basepoint homomorphism β_hdepends only on the homotopyclass of h.

3. For a path-connected space X, show that π₁(X) is abelian iff all basepoint-changehomomorphismsβ_hdepend only on the endpoints of the path h.

4. Show that for a space X, the following three conditions are equivalent:

(a) Every map S¹→X is homotopic to a constant map, with image a point.

(b) Every map S¹→X extends to a map D²→X.

(c) π₁(X,x₀) = 0 for all x₀∈X.

5. Does the Borsuk-Ulam theorem hold for the torus? In other words, for every mapf :S¹×S¹→R² must there exist (x,y) ∈S¹×S¹ such that f (x,y) = f (-x,-y)?

6. From the isomorphism π₁(X×Y, (x₀,y₀)) ≈ π₁(X,x₀)×π₁(Y,y₀) it follows that

7. loops in X×{y₀} and {x₀}×Y represent commuting elements of π₁(X×Y, (x0,y0).Construct an explicit homotopy demonstrating this.

8. If X₀ is the path-component of a space X containing the basepointx₀ , show thatthe inclusion X₀?X induces an isomorphism π₁(X₀,x₀)→π₁(X,x₀).

9. Show that every homomorphism π₁(S¹)→π₁(S¹) can be realized as the inducedhomomorphism ?∗of a map ?: S¹→S¹ .

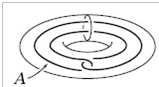
10. Show that there are no retractions r :X→A in the following cases:

(a)  X = R³ with Aany subspace homeomorphic to S¹ .

(b)  X = S¹×D² with A its boundary torus S¹×S¹ .

(c)   X = S¹×D² and A the circle shown in the figure.

(d)  X = D²∨D² with A its boundary S¹∨S¹ .

(e) X the Möbius band and Aits boundary circle.