Reference no: EM13371776
1. Consider the integral
Express this integral in terms of one or more integrals in the order dz dx dy.
2. Consider a regular octahedron, centred at the origin, with vertices at (±1, 0, 0), (0,±1, 0), (0, 0,±1).
(a) Express the volume of this region as a single triple integral in rectangular coordinates.
(b) Express the volume of this region as a single triple integral in cylindrical coordinates.
(c) Express the volume of this region as a single triple integral in spherical coordinates.
(d) Find the ratio of the volume of the octahedron to the volume of the smallest sphere that can enclose it.
3. Consider a circular disc of radius 1 and thickness 1/10 which has a uniform density p(x, y, z) = 1.
(a) Find the moment of inertia of this disc about its central axis (that is, the line joining the centres of its two circular sides).
(b) What is the relationship of the moment of inertia about the central axis to the thickness of the disc?
4. Consider the polar coordinate transformation x = rcosθ , y = rsinθ as discussed in lectures, and let f(x, y) be a given di erentiable function.
(a) Use the chain rule to give expressions for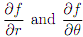
in terms of 
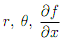and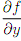 
.
(b) Rearrange your answer to part (a) to give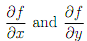 
in terms of 
.
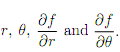(c) Use your answer to part (b) to show that
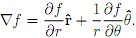
Make sure that you give explicit expressions for the orthogonal unit vectors ^r and ^θ . Show all working.
5. (a) Evaluate the line integral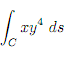 
where C is the right half of the circle x2 + y2 = 16. Show all working.
(b) Evaluate the line integral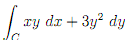 
where C is the curve parameterised by r(t) = 11t4i + t3j, 0≤ t≤ 1. Show all working.
(c) Evaluate the line integral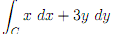
where C is the curve parameterised by r(t) = sin(Πt4)i + cos(Πt3)j, 0≤ t ≤ 1. Show all working
6. The position of an object with mass m at time t is given by
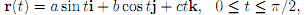
where a, b and c are constants. Find the work done on the object during this time period. Show all working.