Reference no: EM13374776

1) A friend whom you are studying with for this class has drawn three sets of indifference curves. Explain what he has done wrong on each graph and what assumption of preferences is violated by each particular graph.

    (a)                                                    (b)                                                       (c)

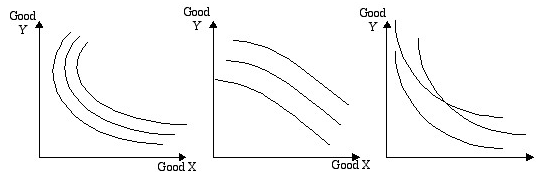
1)  _____________

2) A consumer buys food (F) and shelter (S). If the consumer's income rises and there is no change in the prices of F or S, the marginal rate of transformation of F for S will       

2) _______

A) increase.

B) stay the same.

C) decrease.

D) change, but there is not enough information to know how.

3) Clifford lives by the motto "Eat drink and be merry today, for tomorrow doesn't matter." If today's consumption is represented by "x" and tomorrow's consumption is represented by "y", then which of the following best represents Clifford's utility function? 

3) _______

A) U = x                B) U = x - y           C) U = x/y             D) U = y

4) Which of the following utility functions has the same MRS as U(q1,q2) = q1 q2?     4) _______

A) (q11/2 + q11/2)2            B) q1+ q2              C) q11/2 + q21/2 D) q11/2 q21/2

5) Sarah has the utility function U(X,Y)=X.5Y.25.  When Sarah consumes X=2 and Y=6 she has a marginal rate of substitution of                5) _______

A) -6       B) -12     C) -1/6   D) -1/12

6) If two bundles are on the same indifference curve, then  6) _______

A) no comparison can be made between the two bundles since utility cannot really be measured.

B) the MRS between the two bundles equals one.

C) the consumer derives the same level of utility from each.

D) the consumer derives the same level of ordinal utility from each but not the same level of cardinal utility.

7) If a consumer prefers Apples to Bananas and prefers Bananas to Citrus Fruit, in order to satisfy assumptions about preferences she has to prefer                7) _______

A) Citrus Fruit to Bananas.            B) Bananas to Apples.

C) Apples to Citrus Fruit.                D) Citrus Fruit to Apples.

8) The assumption of completeness means that     8) _______

A) more of a good is always better.

B) the consumer can rank all possible consumption bundles.

C) the consumers can rank all affordable consumption bundles.

D) all preferences conditions are met.

9) The principle that "More is better" results in indifference curves  9) _______

A) sloping down.

B) reflecting greater preferences the further they are from the origin.

C) not intersecting.

D) All of the above.

10) If the price of one good increases while the price of the other good and the consumer's income remain unchanged, what will happen to the budget line?             10) ______

A) The budget line shifts outward without a change in slope.

B) The budget line shifts inward without a change in slope.

C) The budget line rotates outward from the intercept on the axis of the good that did not change in price.

D) The budget line rotates inward from the intercept on the axis of the good that did not change in price.

               

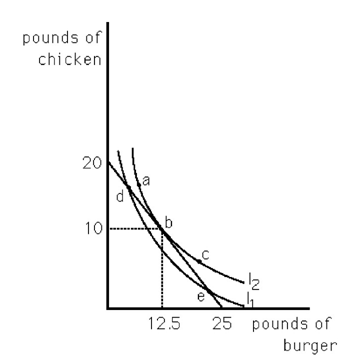
11) Max has allocated $100 toward meats for his barbecue. His budget line and an indifference map are shown in the above figure. What is the price of chicken?           11) ______

A) $1.25/lb           B) $0.80/lb            C) $5/lb D) $4/lb

12) Suppose Joe's utility for lobster (L) and soda (S) can be represented as U =L^0.5S^0.5. Joe walks into a restaurant with $72. Lobsters cost $18 each and sodas cost $2 each. How much lobster and soda will Joe consume if he intends to spend all his money? (There are no tax and no tips.)

13) The consumer is in equilibrium when                13) ______

A) the budget line is tangent to the indifference curve at the bundle chosen.

B) MRT = MRS.

C) P_x/P_y = MU_x/MU_y.

D) All of the above.

 

14) Jezz has the quasi log-linear utility function

                U(q1,q2) = q1+ 2ln(q2)

Jezz has an income of $100 and faces prices p1= p2= 20. 

a.     What is the marginal rate of substitution for this utility function?

b.     Solve for Jezz's optimal bundle.

c.     Suppose Jezz's income falls to $20.  What will happen to his optimal bundle?  Is the MRS=MRT at the optimal bundle?

14)  _____________

15) If the consumer's income increases while the prices of both goods remain unchanged, what will happen to the budget line?                15) ______

A) The budget line rotates outward from the intercept on the vertical axis.

B) The budget line shifts inward without a change in slope.

C) The budget line rotates inward from the intercept on the horizontal axis.

D) The budget line shifts outward without a change in slope.

16) Suppose Charley only purchases boardgames (B) and haircuts (H) with his income.  If the price of boardgames increases by 100% while the price of haircuts increases by 300%, how will the MRT change (consider the budget constraint drawn on a graph with boardgames on the horizontal axis)?

16)  _____________

17) If both prices decreases by 50%             17) ______

A) slope of the budget constraint will decrease.

B) budget constraint will be unchanged.

C) budget constraint will shift outward in a parallel fashion.

D) slope of the budget constraint will increase.

18) Joe's income is $500, the price of food (F) is $2 per unit, and the price of shelter (S) is $100. Which of the following represents his budget constraint?     18) ______

A) 500 = 100F + 2S             B) S = 500 - 2F

C) 500 = 2F + 100S             D) All of the above.

 

               

19) Max has allocated $100 toward meats for his barbecue. His budget line and an indifference map are shown in the above figure. What happens if Max receives a $100 cash grant to buy either meat or chicken?           19) ______

A) Max will spend it all on burger. Because of its lower price, he can buy more of it.

B) Max will take advantage of the gift by buying all chicken because it is the more expensive meat.

C) Max will double his consumption of both meats.

D) There is not enough information to answer the question.

20) Howie consumes only beer (B) and donuts (D) each week with his $100 income.  Beer costs $1, while donuts cost only 50¢.  Howie has Cobb-Douglas preferences given by:

                                U(B,D) = B(D-d)

where d is the quantity of donuts that his neighbor Nord consumes.  Assume throughout this question that Howie always consumes more donuts than Nord. 

a.  How does Nord's beer consumption influence Howie's utility function?  Specifically, compute and determine the sign of ∂U/∂d.  Intuitively, what does this tell you about Howie's happiness and Nord's consumption of donuts?

b.  Holding d fixed, compute Howie's optimal consumption bundle of Beer and Donuts as functions of Nord's consumption of donuts, d.

c.  How does Nord's consumption of donuts affect Howie's optimal bundle?  Specifically calculate and determine the sign of ∂B*/∂d and ∂D*/∂d where (B*,D*) is Howie's optimal consumption bundle.

20)  _____________

21)-23) P95 in the textbook, #25, #38, #39

1) The first graph (a) has portions that are upward instead of downward sloping, which implies a consumer can consume so much of Y that they are actually made worse off from more units (satiation). Thus this violates the assumption that more is better. The second graph (b) violates convexity since the curves are bowed outward instead of inward towards the origin.  The last graph (c) violates transitivity since the indifference curves are intersecting one another.  If they cross, then all points on both indifference curves are equally preferred.  But then points exist which are on the same indifference curve but contain less of each good.

2) B

3) A

4) D

5) B

6) C

7) C

8) B

9) D

10) D

11) C

12) Maximizing Joe's utility subject to his budget constraint yields:

U =L^0.5S^0.5+l(72 - 18L - 2S)

1. dU/dL= 0.5 L^0.5S^0.5- l18 = 0

2. dU/dL= 0.5 L^0.5S^0.5- l2 = 0

3. dU/dL= 72 - 18L - 2S = 0

From 1) and 2), S/L = 9 or S = 9L. Substituting into 3) yields 72 - 36L = 0 or L = 2. Since S = 9L, S = 18. Thus Joe will buy two lobsters and wash it all down with 18 sodas.

13) D

14) a.     MRS = U1/U2= 1/(2/q2) = .5q2

b. Set MRS=MRT  .5q2=1  q2= 2

 With his remaining income ($60) he will purchase q1= 3

c. He can no longer afford q2=2, and so will choose q2= 1 and q1= 0.  This is a corner solution and the MRS is not equal to the MRT.

15) D

16) Before the price change, the MRT=-pB/pH.  After the price change, the MRT'=-(2)pB/(4)pH=MRT/2.  The MRT is half. 

17) C

18) C

19) C

20) a.  The derivative is -B, meaning Howie's utility decreases as Nord consumes more donuts (holding all else fixed).  Howie apparently does not like to see Nord consume donuts.

b.  D*=100+.5d, B*=50-.25d.

c.  ∂B*/∂d=-.25<0 and ∂D*/∂d=.5>0.  As Nord consumes more donuts, Howie will consume more donuts and less beer.