Reference no: EM13371499

1. One single number digit is selected randomly,
a. List the sample space.
b. What is the probability of each event?
c. What is the probability of an even number?

2. A bowl contains two kinds of identical-looking, foil wrapped, chocolate egg shaped candies. All but 42 of them are milk chocolate and all but 35 are dark chocolate.

a. How many of each kind are in the bowl?

b. How many candies are there in the bowl?

c. If one chocolate is selected at random, what is the probability that it is a milk chocolate?

d. If one chocolate is selected at random what is the probability that it is milk or dark chocolate?

e. If one chocolate is selected at random, what is the probability that it is milk and dark chocolate?

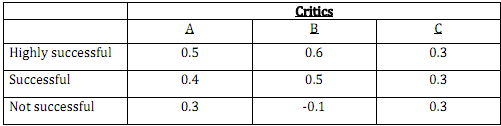
3. Let x be the success rating of the new television show. The following table lists the subjective probabilities assigned to each x for a particular new show by three different media critics. Which of the following three sets of probabilities are inappropriate because they violate a basic rule of probability? Explain

4. An experiment consists of two trials. The first is tossing a penny and observing weather it lands with heads or tails facing up; the second is rolling a die and observing a 1,2,3,4,5 or 6.

a. Construct a sample space using a tree diagram.

b. List your elements as ordered pairs, with the first element representing the coin and the second, the die.

5. A group of files in medical clinic classifies the patients by gender and by type of diabetes (type 1 or type 2). The groupings may be shown as follows. The table gives the number in each classification.

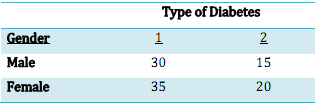
a. Display information on this 2x2 table as a Venn diagram using "type1" and male as the two events displaying as circles.

b. The selected individual is female.

c. The selected individual has type 2 diabetes.

6. A box contains four red and three blue poker chips. Three poker chips are to be randomly selected, one at a time.

a. What is the probability that all three chips will be red if the selection is done with replacement?

b. What is the probability that all three chips will be red if the selection is done without replacement?

c. Are the drawings independent in either part a or b? justify your answer.

7. You have applied for two scholarships: a merit scholarship (M) and an athletic scholarship (A). Assume the probability that you receive the athletic scholarship is 0.25, the probability that you receive both scholarships is 0.15 and the probability that you get atleast one of the scholarships is 0.37.
a. What is the probability that you receive the merit scholarship?

b. What is the probability that you do not receive either of the two scholarships?

c. What is the probability that you receive the merit scholarship, given that you have awarded the athletic scholarship?

d. What is the probability that you receive the athletic scholarship, given that you have been awarded the merit scholarship?

8. If P(A)=0.4, P(B)=0.5, and P(A and B)=0.1, find P(A or B).

9. P(A)=0.3, P(A or B) = 0.9, and P(A and B)= 0.1, find P(B).

10. A and B are events defined on a sample space, with P(A|B)=0.5 and P(B)=0.8. Find P(A and B).

11. Juan lives in a large city and commutes to work daily by subway or by taxi. He takes the subway 80% of the time because it costs less, and he takes taxi the other 20% of the time. When taking the subway, he arrives at work on time 70% of the time, where as he makes it on time 90% of the time when he travels by taxi.

a. What is the probability that Juan took the subway and is at work on time on any given day?

b. What is the probability that Juan took a taxi is on time on any given day?

12. The following table shows the sentiments of 2500 wage-earning employees at Spruce company on a proposal to emphasize fringe benefits rather than wage increases during their impending contract discussions.

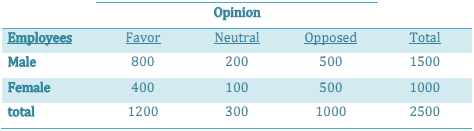
a. What is the probability that an employee selected at random from this group will be opposed.

b. Calculate the probability that an employee selected at random from this group will be female.

c. Calculate the probability that an employee selected at random from this group will be opposed, given that the person is male.

d. Are the events "opposed" and "female" independent? Explain.