The Z-transform of delayed truncated sequence The one-sided z-transform of

x(n) is given by

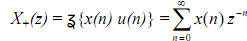
Given sequence x(n), we delay it by k units, and then truncate it to left of n = 0 to get x(n-k) u(n). We want to find the z-transform of x(n-k) u(n).

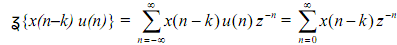
If we let n-k = r, then n = r+k, and summation limits n = 0 to ∞ become r = -k to ∞. Then

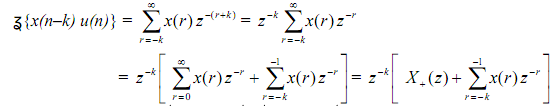
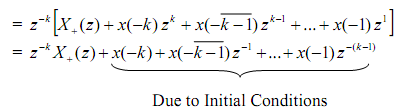
Refer to X+(z) as X(z) and write the result as

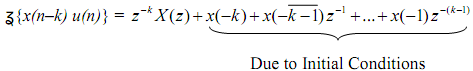
The result shown above is used to solve linear constant coefficient difference equations with inputs that are stepped into a system. Suppose that we want solution of

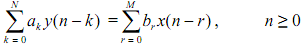
subject to initial conditions

{y(i), i = -1, -2, ..., -N}         and      {x(i), i = -1, -2, ..., -M}

We take z-transform of the equation using the result derived above for delayed-truncated sequences

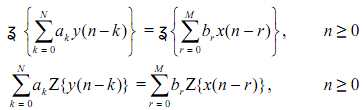
here we have used Z to mean ? the z-transformation operation. The left hand side is given by

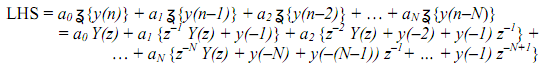
(In terms of the derivation earlier all the Y(z)'s are Y+(z)'s, that is , one-sided transforms). All the Y(z) terms are grouped together under a summation, and all the remaining terms, because of the initial conditions {y(i), i = -1, -2, ..., -N}, can be grouped together such that the above can be written as

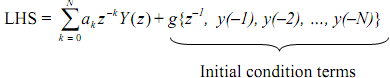
By following a similar procedure the right hand side can also be written as follows (here again the X(z)'s are X+(z)'s, i.e. , one-sided transforms):

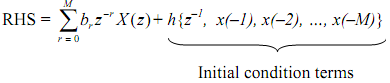
LHS = RHS becomes

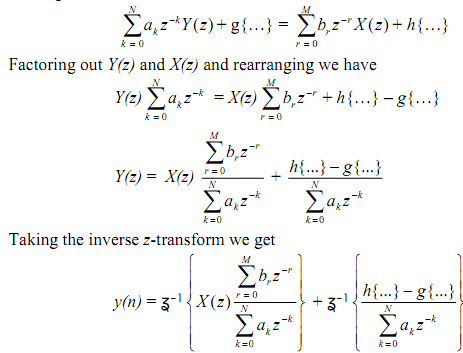
To summarize: to solve for y(n) we take the z-transform of linear constant coefficient difference equation by using initial conditions, manipulate in the z-domain to get Y(z) and then take the inverse z-transform of Y(z) to obtain y(n).

Example Find the solution to

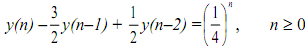
with initial conditions y(-1) = 4, y(-2) = 10.

Solution There are 3 methods of solution:

1.   Find iterative solution in discrete-time domain. Generally this will not give an analytical form of solution.

2.   Solve in discrete-time domain (homogeneous solution + particular solution).

3.   Solve in frequency domain as shown below.

For the input sequence x(n) which is stepped into a system, specified in words such as x(n) = 0 for n < 0, the initial conditions are zero and do not matter. But for the output sequence y(n) where the initial conditions y(-1), y(-2) are explicitly given to be non-zero we are required to use the above derived "z-transform for the delayed truncated sequence". Particularly we have

 
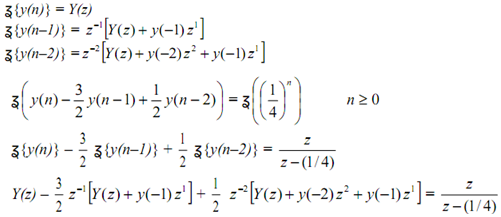
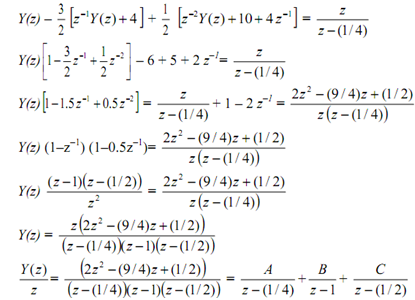
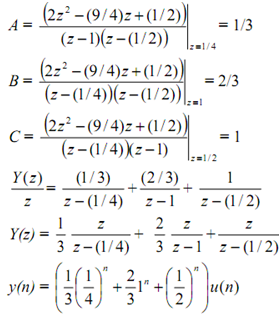
The time-domain solution was covered in HW. The solution is repeated below

Email based Z-transform of delayed truncated sequence assignment help - Z-transform of delayed truncated sequence homework help at Expertsmind

Are you finding answers for Z-transform of delayed truncated sequence based questions? Ask Z-transform of delayed truncated sequence questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Z-transform of delayed truncated sequence assignment help -Z-transform of delayed truncated sequence homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours