z-transform and realization of digital filters:

For the continuous-time systems Laplace transform is an extension of Fourier transform. The Laplace transform can be applied to a broader range of signals which the Fourier transform can, since there are a number of signals for which the Fourier transform doesn't converge but the Laplace transform does. The Laplace transform allows us, for instance, to perform transform analysis of unstable systems and to develop additional insights and tools for LTI system analysis.

Z-transform is the discrete time counterpart of the Laplace transform. The z- transform enables us to analyze certain discrete-time signals which do not have a discrete-time Fourier transform. The properties and motivations of the z-transform nearly resemble those of the Laplace transform. But, as with the relationship of continuous time versus the discrete-time Fourier transforms, there are distinctions in between the Laplace transform and the z- transform.

Definition 

The two-sided or bilateral z-transform, X(z), of the sequence x(n) can be defined as

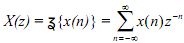
where z = r e^jw is complex variable. The above power series is a Laurent series.

The one-sided or unilateral z-transform can be defined as

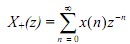
The unilateral z-transform is specifically useful in analyzing causal systems specified by the linear constant-coefficient difference equations having nonzero initial conditions into which the inputs are stepped. It is widely used in digital control systems.

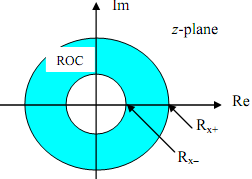
The region of convergence (ROC) 

It is the set of z values for which the above summation converges. Generally the ROC is an annular region in complex z-plane which is given by

ROC = Rx_- < |z| < Rx₊

The relationship in between z-transform and discrete-time Fourier transform Setting z = r e^jw by definition

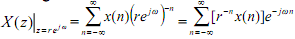
If |z| = r = 1, then z-transform, obtained on the unit circle, vides the discrete-time Fourier transform of sequence x(n), which means that

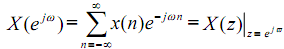
Example: The positive-time signal

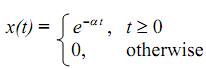
is sampled at T-second intervals resulting in series x(nT) or x(n)

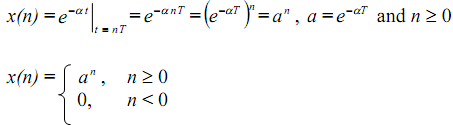
If a < 1 this series decays exponentially to 0 as n → ∞. By substituting x(n) in the equation, the z-transform is

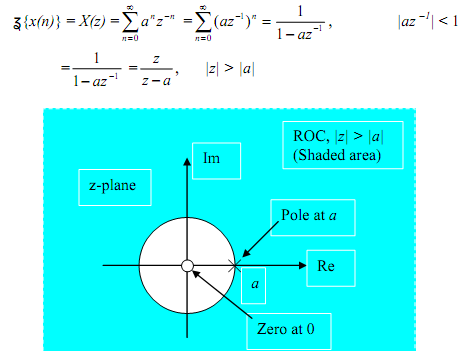
The ROC is |z| > |a|. It is X(z) is a rational function (a ratio of polynomials in z). The roots of numerator polynomial are zeros of X(z) and roots of denominator polynomial are poles of X(z).

It is a right-sided sequence. Right-sided sequences have a ROC which is the exterior of a circle having radius Rx- (|z| > |a| in this). If ROC is the exterior of a circle it is a right- sided series.

Email based z-transform and realization of digital filters assignment help - z-transform and realization of digital filters homework help at Expertsmind

Are you finding answers for z-transform and realization of digital filters based questions? Ask z-transform and realization of digital filters questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer z-transform and realization of digital filters assignment help -z-transform and realization of digital filters homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours