Window functions We want to take the frequency nature of window functions by themselves. Note that relaying on convenience we may describes the window functions either over - (N-1)/2 ≤ n ≤ (N-1)/2 or over 0 ≤ n ≤ (N-1). In the former type the phase method will be zero; in the latter type, used mainly in MATLAB, the phase has a negative tangent slope.
There are normal four types of windows and adjustable windows. Among the fixed windows we have the given tapered windows:
1. Bartlett (triangular) window
2. Hann (aka Hanning or von Hann) window
3. Hamming window
4. Blackman window
These windows give in a fixed value of ripple in the frequency response of the described filter. The Kaiser window is an adjustable window which gives some control over the ripple.
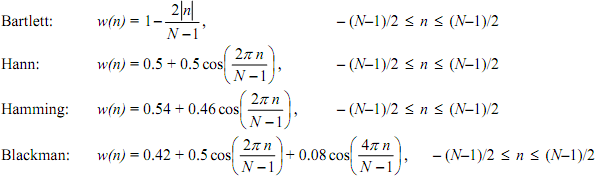
The following MATLAB multiplot provides a graphical relation of the above window functions. Note that all are discrete linear sequence; to create it easy on the eyes some are given as various lines and some as discrete.
%Window functions defined over n = -(N-1)/2 to (N-1)/2
N = 31; n = -(N-1)/2: (N-1)/2;
wR = n-n+1; %Rectangular
wBa = 1 - 2* abs(n)/(N-1); %Bartlett
wHn = 0.5 + 0.5 * cos(2*pi*n/(N-1)); %Hamming wHm = 0.54 + 0.46 * cos(2*pi*n/(N-1)); %Hamming
wBl = 0.42 + 0.5 * cos(2*pi*n/(N-1)) + 0.08 * cos(4*pi*n/(N-1)); %Blackman
%Multiplot. All are discrete sequences.
%To make it easy on the eyes some are plotted with continuous lines. plot (n, wR, 'o', n, wBa, 'b', n, wHn, 'k', n, wHm, 'b*', n, wBl, 'k--'); legend ('Rectangular', 'Bartlett', 'Hanning', 'Hamming', 'Blackman'); xlabel('n'), ylabel('w(n)'); grid; title ('Window functions')
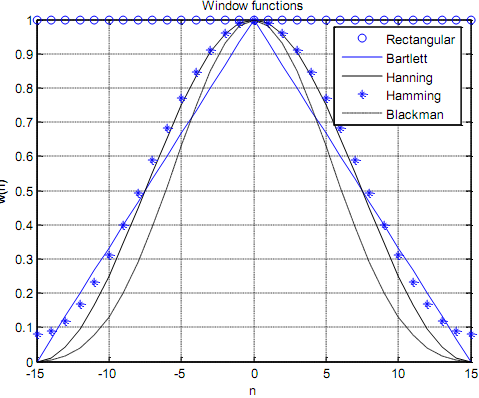
%Window functions defined over n = -(N-1)/2 to (N-1)/2
N = 31; n = -(N-1)/2: (N-1)/2;
wHn = 0.5 + 0.5 * cos(2*pi*n/(N-1)); %Hanning wHm = 0.54 + 0.46 * cos(2*pi*n/(N-1)); %Hamming
wBl = 0.42 + 0.5 * cos(2*pi*n/(N-1)) + 0.08 * cos(4*pi*n/(N-1)); %Blackman
%
subplot(3, 1, 1), stem(n, wHn); legend ('Hanning');
xlabel('n'), ylabel('w(n)'); grid
subplot(3, 1, 2), stem(n, wHm); legend ('Hamming');
xlabel('n'), ylabel('w(n)'); grid
subplot(3, 1, 3), stem(n, wBl); legend ('Blackman');
xlabel('n'), ylabel('w(n)'); grid
Email based Window functions in Design of FIR digital filters assignment help - Window functions in Design of FIR digital filters homework help at Expertsmind
Are you finding answers for Window functions in Design of FIR digital filters based questions? Ask Window functions in Design of FIR digital filters questions and get answers from qualified and experienced Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Window functions in Design of FIR digital filters assignment help -Window functions in Design of FIR digital filters homework help and Digital signal processing problem's solution with step by step procedure.
Why Expertsmind for Digital signal processing assignment help service
1. higher degree holder and experienced tutors
2. Punctuality and responsibility of work
3. Quality solution with 100% plagiarism free answers
4. On Time Delivery
5. Privacy of information and details
6. Excellence in solving Digital signal processing queries in excels and word format.
7. Best tutoring assistance 24x7 hours