The property of liquids (or gases) by virtue of which a backward dragging force (viscous drag) acts tangentially on the layers of the liquid in motion and it tries to stop the motion is known as viscosity. The effect of viscosity is similar as the effect of friction between the solids as it opposes the flow of fluids.
|
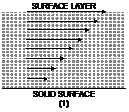
Coefficient of Viscosity: Consider a liquid steadily flowing over a horizontal solid surface in the form of parallel layers This flow is called as laminar flow. The surface in contact with the solid surface is found to be at rest and as we goes up, the velocity of the layers reaches on increasing and the layer at the top possesses maximum velocity.
|
|
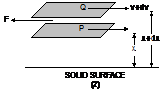
Let us consider two parallel layers P and Q at distances x, x + dx from the solid surface moving with the velocities v and v + dv respectively (Fig. 2). Then dv/dx denotes the rate of change of velocity with the distance in the direction of increasing distance and it is called the velocity gradient. The related rotation between the two sides can take place only, if some outer friction force operates between them. Because of viscosity, a force F acts in opposite direction to oppose the relative motion. According to Newton, the viscous force F relays upon the given factors:
1. It is directly proportional to the area of the layers in touch i.e. F ∝ A
2. It is directly proportional to the velocity gradient between each layers i.e.F ∝ dv/dx
Combining these two factors, we have, F ∝ Adv/dx or F = -nadv/dx ..... (i)
where h is a constant depending upon the nature of the liquid and is called the coefficient of viscosity. The negative value denotes that the viscous force is directed in a direction opposite to the direction of the motion of the liquid. If A=1 and dv/dx=1, then from equation (i), we get, h = F
Hence, the constant coefficient of viscosity of a liquid may be described as the tangential viscous force, which maintains a unit velocity gradient between its two parallel parts, each of unit area.
In cgs system, the unit of h is dyne-sec cm-2 or g-cm-1 s-1, called poise.
The coefficient of viscosity of a liquid is called one poise, if a tangential force of 1 dyne maintains a velocity gradient of 1 s-1 between two parallel layers each 1 cm2 in area.
In SI, the unit of h is N-s m-2 or kg m-1 s-1, called decapoise.
The coefficient of viscosity of a liquid is called one decapoise, if a tangential force of 1 N maintains a velocity gradient of 1 s-1 between two parallel layers, each 1 m2 in area.
1 decapoise = 1 N s m-2 = (105 dyne) ´ 1s ´ (100 cm)-2 = 10 poise
The dimensional mathematical relation of coefficient of viscosity is [M L-1 T-1]
Poiseuille's formula:
Flow of viscous liquid through a capillary tube (Poiseuille's formula)
The velocity v at a distance y from the capillary axis for a flow of liquid of viscosity h in a capillary tube of length L and radius r under a pressure difference P across it is given by , 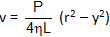
and the volume of liquid flowing per second is given by , 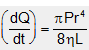 .
.
Stokes' Formula:
When a spherical object falls through the fluid, layer in immediate touch with it, sticks to it and goes along with the object with the similar speed. The layer next to it has lower speed, the next still lesser and so on, while the part at a considerable distance from the object remains at rest. As a result of this relative rotation, a backward dragging force is set up, which repels the motion of the object. This backward dragging tension, called the viscous force. As the object falls, its speed goes on increasing and likewise the viscous force on the object becomes same to the weight of the object. Then, the object goes with a constant speed, called terminal speed. Stokes found that when the object attains terminal speed, the viscous force on the object is shown by, F = 6 p h r v .... (i)
Here h, r and v respectively shows the coefficient of viscosity of the fluid, radius of the spherical object and the terminal velocity attained by the object. The relation (i) is called as Stokes' law.
Terminal velocity:
When a spherical body goes through a viscous fluid, it feels a viscous force. The value of the viscous force increases with the increase in speed of the object falling under the function of its weight. As a result, the viscous force soon becomes the driving force and the object starts rolling with a constant speed, known as its terminal velocity. Let us now produce an relation for the terminal velocity, as an application of stokes' principle.
Email based Physics assignment help - homework help at Expertsmind
Are you searching physics expert for help with Viscosity questions? Viscosity topic is not easier to learn without external help? We at www.expertsmind.com offer finest service of Physics assignment help and physics homework help. Live tutors are available for 24x7 hours helping students in their Viscosity related problems. We provide step by step Viscosity question's answers with 100% plagiarism free content. We prepare quality content and notes for Viscosity topic under physics theory and study material. These are avail for subscribed users and they can get advantages anytime.
Why Expertsmind for assignment help
- Higher degree holder and experienced experts network
- Punctuality and responsibility of work
- Quality solution with 100% plagiarism free answers
- Time on Delivery
- Privacy of information and details
- Excellence in solving physics queries in excels and word format.
- Best tutoring assistance 24x7 hours