Useless Productions  in  Context-Free Grammars:

Given a context free grammar G = (V, Σ, P, S), it may have rules which are useless for a number of reasons. For instance, consider the grammar G₃  = ({E, A, a, b}, {a, b}, P, E), where P is set of rules

E -→ aEb,

E -→ ab,

E -→ A,

A -→ bAa.

The basic problem is that nonterminal A  does not derive the terminal strings, and hence, it is useless, as well as the last 2 productions.  Now let us consider the grammar G₄ = ({E, A, a, b, c, d}, {a, b, c, d}, P, E), where P is set of rules

E -→ aEb,

E -→ ab,

A -→ cAd,

A -→ cd.

This time, nonterminal A generates strings of the form cⁿ dⁿ, but there is no derivation E 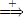 α from E where A occurs in α. The nonterminal A is not connected to E, and the last 2 rules are useless. Fortunately, it is possible to find this type of useless rules, and to eliminate them.

Let T (G) be the set of nonterminals which actually derive some terminal string, that is

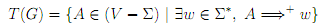
The set T (G) is defined by stages. We de?ne the sets T_n  (n ≥ 1) as follows:

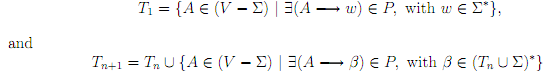
It is simple to prove that there is some least n  such that T_n+1= T_n , and that for this n, T (G)= T_n .

If S ∈/ T (G), then L(G)= ∅, and  G is equivalent to trivial grammar

G' = ({S}, Σ, ∅, S).

If S ∈ T (G), then let U (G) be the set of nonterminals that  are useful, that is,

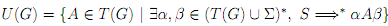
The set U (G) can be computed by stages also. We define the sets Un  (n ≥ 1) as follows:

It is simple to prove that there is least n  such that U_n+1= U_n , and that for this n, U (G) = U_n ∪ {S}.  Then, we can use U (G) to transform G into an equivalent CFG in which every nonterminal is useful (that is, for which V - Σ= U (G)). Simply delete all rules having symbols not in U (G).  We say that a context-free grammar G is reduced if all its nonterminals are useful, that is, N = U (G).

It should be kept in mind that although dull, the above considerations are essential in practice. Algorithms for constructing parsers, for instance, LR-parsers, may loop if useless rules are not eliminated! Consider the other normal form for context-free grammars, the Greibach Normal Form.

Email based Automata assignment help - homework help

The study of automata is an important area of theory of computation. Students feel trouble in solving automata questions. We at www.expertsmind.com offers Automata assignment help - Automata homework help and online tutoring with best qualified and experienced computer science tutor's help. We cover all topics including Useless Productions in Context-Free Grammars in assignment help - homework help service. Get solved problems in automata theory with step by step answers anytime from expert tutors at expertsmind.