The unit step sequence

u(n) =    1,       n≥ 0

     0,      n < 0

u(argument) =    1, if argument ≥ 0

 0, if argument < 0

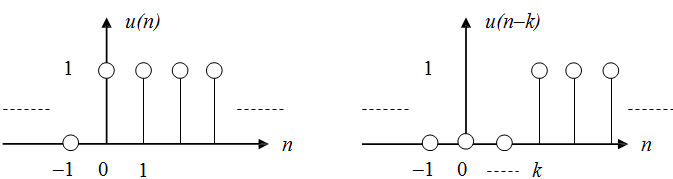
a) The discrete delta function can be defined as the 1st difference of the unit step function:

δ(n) = u(n) - u(n-1)

b) The sum from -∞ to n of the δ function gives the unit-step as follows:

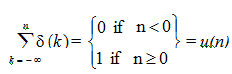
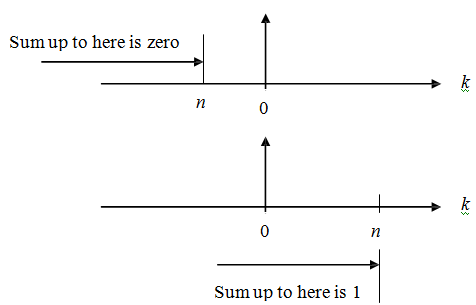
Results (a) and (b) are similar to the continuous-time derivative and integral respectively.

c) By going through the graph of u(n), which is shown below, we can write:

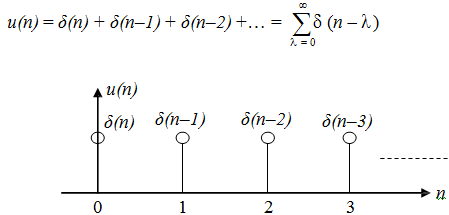
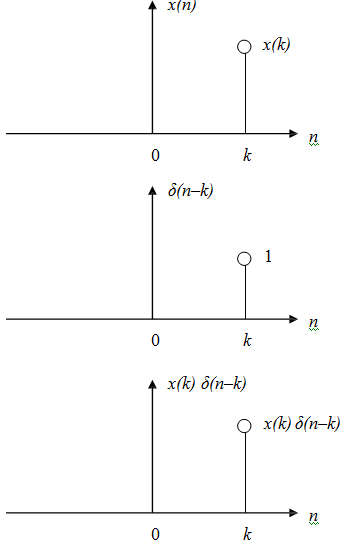
d) For any of the arbitrary sequence x(n), we have

x(n) δ(n-k) = x(k) δ(n-k)

which means that, the multiplication will pick out only one value x(k).

 If we find out the infinite sum of the above equation we get the sifting property:

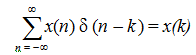
e) We can express x(n) as follows:

x(n) = ...+ x(-1) δ(n+1) + x(0) δ(n) + x(1) δ(n-1) + x(2) δ(n-2) + ...

This true for all n by setting in turn

..., n = -2, n = -1, n = 0, n = 1, n = 2, etc. ... The above formula can be written compactly as follows

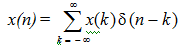
This is a weighted-sum of the unit sample functions which were delayed.

Email based Unit step sequence assignment help - Unit step sequence homework help at Expertsmind

Are you finding answers for Unit step sequence based questions? Ask Unit step sequence questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Unit step sequence assignment help -Unit step sequence homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours