Types of sets:
Null or Empty Set
A set which has no element is called the null set or empty set and is denoted by Φ (phi). The number of elements of a set A is denoted as n (A) and n (Φ) = 0 as it has no element. For example the set of all real numbers whose square is -1.
Singleton set
A set having only one element is defined as Singleton Set.
Finite and infinite set
A set, which has limited numbers of members, is called as finite set. Otherwise it is known as an in finite set. As like, the set of all weeks in a year is a finite set whereas; the set of all real number is an infinite set.
Union of sets
Union of two or more than two sets is the set of all components that related to any of these sets. The symbol taken for union of sets is ∪ i.e. A∪B = Union of set A and set B = {x: x∈A or x∈B}
Problem: A = {1, 2, 3, 4} and B = {2, 4, 5, 6} and C = {1, 2, 6, 8}, then A∪B∪C = {1, 2, 3, 4, 5, 6, 8}
Intersection of sets
It is the set of all the members, which are usual to all the sets. The symbol shown for intersection of sets is '∩' i.e. A ∩ B = {x: x ∈A and x∈B}
Problem: If A = {1, 2, 3, 4} and B = {2, 4, 5, 6} and C = {1, 2, 6, 8}, then A ∩ B ∩ C = {2}
Difference of sets
The difference of set A to B shown as A - B is the set of those members that are in the set A but not in the set B i.e. A - B = {x: x∈A and x∉B}
Equally B - A = {x: x∈B and x∉ A}
In usual A-B ≠ B-A
Problem: If A = {a, b, c, d} and B = {b, c, e, f} then A-B = {a, d} and B-A = {e, f}.
Symmetric Difference of Two Sets:
For two sets B and A, symmetric difference of B and A is provided by (A - B) ∪ (B - A) and is shown by A Δ B.
Subset of a set
A set A is called be a subset of the set B if each and every element of the set A is also the member of the set B. The symbol taken is '⊆' i.e. A ⊆ B <=> (x ∈ A => x ∈ B).
Each and every set is a subset of its own set. Also a void set is a part of any set. If there is at least one member in B which does not related to the set A, then A is a proper subset of set B and is shown as A⊂B. e.g If A = {a, b, c, d} and B = {b, c, d}. Then B⊂A or similarly A⊃B (i.e A is a super set of B). Total number of group or subsets of a finite set containing n members is 2n.
Equality of Two Sets:
Sets A and B are called equal if A ⊆ B and B ⊆ A; we can write A = B.
Universal Set:
A non-empty set or group of which all the sets under concern are subsets is known as the universal set. In any kind of application of set theory, all the sets under concern may likely to be subsets of a set known as Universal Set. As name shows it is the set with collection of all the parts and generally denoted by 'U'.
e.g. (1) set of real numbers R is a universal set for the operations associated to real numbers.
Complementary set:
The complement of a set A with related to the Universal Set U is difference of U and A. Complement of set A is shown by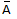 
(or AC) (or A'). Therefore is the set of all the members of the Universal Set which do not relates to the set A.
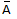= U - A = {x: x ∈ U and x ∉ A}
we may say that A U 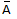= U (Universal Set) and A ∩ 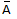= Φ (Void Set)
Email based Types of sets Assignment Help -Types of sets Homework Help
We at www.expertsmind.com offer email based Types of sets assignment help - homework help and projects assistance from k-12 school level to university and college level and engineering and management studies. We provide finest service of Mathematics assignment help and Mathematic homework help. Our experts are helping students in their studies and they offer instantaneous tutoring assistance giving their best practiced knowledge and spreading their world class education services through e-Learning program.
Expertsmind's best education services
- Quality assignment-homework help assistance 24x7 hrs
- Best qualified tutor's network
- Time on delivery
- Quality assurance before delivery
- 100% originality and fresh work