Type of functions:
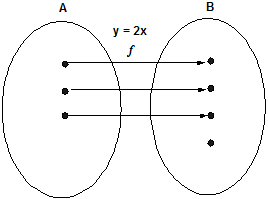
One - One or injective function: A function f: X → Y is called to one - one or injective if every element in the domain of a function has a different image in the co - domain. Example: f:R→R f(x) = 2x is one - one.
Many - one function: A function f: X →Y is called be many one if there are at least two components in the domain whose images are the exact.
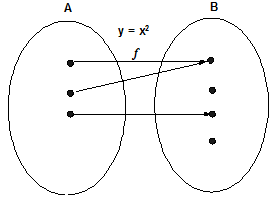
Example: f: R→R shown by f(x) = x2 is Many - one.
METHODS TO CALCULATE ONE - ONE AND MANY - ONE:
- If f(x1) = f (x2) => x1 = x2 for each and every x1,x2 in the domain, then 'f' is one - one else many - one.
- If the function is completely decreasing or increasing in the domain, then 'f' is one - one else many - one.
Graphical Method: If we define a line parallel to the x - axis cut the graph of y = f(x) at one and only single point, then f(x) is one - one and if the line parallel to the x - axis intersect the graph at more than one distinct points then f(x) is a many - one function.
- Any continuous function f(x) which have at least one local minima or local maxima is many - one.
- All even functions have to be many one.
- All polynomials of even degree distinct on R have at least one local maximum or minima and therefore are many one on the domain R. Polynomials of odd degree may be one - one or many - one.
Onto function or Surjective function: A function f: X→Y is called be a onto function or Surjective function if and only if every element of Y is the image of any element of X i. e. if and only if for each y∈Y there exists some x∈X such that y = f(x). Therefore 'f' is onto if f(x) = Y i. e. range = co - domain of function.
Example: The map f: R →[ -1,1] provided by f(x) = sinx is an onto map.
Into function: A function f: X→Y is called an into function if there exists at least one component in the co - domain Y which is not an reflection of any element in the domain X.
Example: The map f: R →R provided by f(x) = x2 is an into map
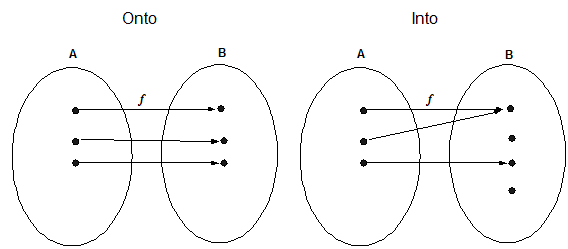
One - one onto map or bijective function: A function f: X →Y is called one - one onto or bijective function if and only if
(i) Different elements of X have different images in Y
(ii) Each element of Y has at least one pre - image in X.
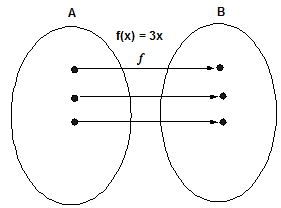
Example: The map f: X→Y provided by f(x) = 2x is a one - one onto map.
Email based Type of functions Assignment Help -Type of functions Homework Help
We at www.expertsmind.com offer email based Type of functions assignment help - homework help and projects assistance from k-12 school level to university and college level and engineering and management studies. We provide finest service of Mathematics assignment help and Mathematic homework help. Our experts are helping students in their studies and they offer instantaneous tutoring assistance giving their best practiced knowledge and spreading their world class education services through e-Learning program.
Expertsmind's best education services
- Quality assignment-homework help assistance 24x7 hrs
- Best qualified tutor's network
- Time on delivery
- Quality assurance before delivery
- 100% originality and fresh work