Tree Domains and Gorn Trees:

Derivation trees play a very significant role in parsing theory and in proof of a strong version of the pumping lemma for context-free languages called as Ogden's lemma. Therefore, it is significant to define derivation trees. We do so by making use of Gorn trees.

Let N₊ = {1, 2, 3,.. .}.

Definition: A tree domain D is the nonempty subset of strings in 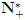 satisfying the conditions:

(1) For all u, v ∈ 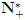, if uv ∈ D, then u ∈ D.

(2) For all u ∈ 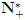, for every i ∈ N₊ , if ui ∈ D then uj  ∈ D for every j,1 ≤ j ≤ i.

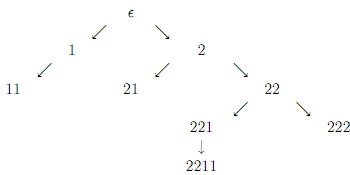
The tree domain

D = { , 1, 2, 11, 21, 22, 221, 222, 2211}

Can be represented as follows:

A tree labeled with symbols from a set Δ is defined as follows.

Definition: Given a set Δ of labels, a Δ-tree is a total function t : D → Δ, where D is a tree domain.

The domain of a tree t is denoted as dom(t).  Every string u ∈ dom(t) is known as tree address.

Assume Δ = {f, g, h, a, b}. The tree t : D → Δ, where D is tree domain of previous example and t is the function whose graph is

{( , f ), (1, h), (2, g), (11, a), (21, a), (22,f ), (221, h), (222, b), (2211, a)}

Can be  represented as follows:

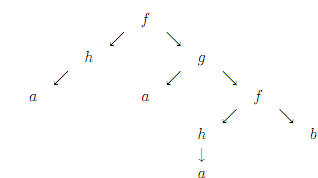
The outdegree (at times called as ramification) r(u) of a node u is cardinality of the set

{i | ui ∈ dom(t)}.

The outdegree of a node can be infinite.  Most of the trees which we shall consider will be finite-branching , that is, for every node u, r(u) will be an integer, and thus finite. If the outdegree of all the nodes in the tree is bounded by n, then we can view the domain of the tree as defined over {1, 2,..., n}*.

The node of outdegree 0 is known as leaf . The node address of which is known as root of the tree. A tree is finite if the domain dom(t) of it is finite. Given a node u in dom(t), every node of the form ui in dom(t) with i ∈ N₊ is called a son of u.

Tree addresses are ordered lexicographically :  u ≤ v if u is a prefix of v or, there exist strings x, y, z ∈  and i, j ∈ N₊, with i < j, such that u = xiy  and v = xjz.

In the 1st case, we say that u is an ancestor of v  and in the 2nd case, that u is to the left of v.

If y = ∈ and z = ∈, we say that xi  is a left brother of xj, (i < j).  Two tree addresses u and v are independent if u is not a prefix of v and v is not a prefix of u.

Given a finite tree t, yield of t is string

t(u1 )t(u2) ··· t(uk ),

where u1 , u2 ,..., uk   is sequence of leaves of t in lexicographic order.

For instance, the yield of tree below is aaab:

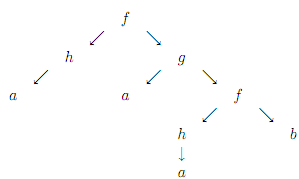
Given a finite tree t, depth of t is integer

d(t)= max{|u|| u ∈ dom(t)}.

Given a tree t and a node u in dom(t), subtree rooted at u is tree t/u, whose domain is the set

{v | uv ∈ dom(t)}

and such that t/u(v)= t(uv) for all v in dom(t/u).

Another significant operation is the operation of tree replacement.

Email based Automata assignment help - homework help

The study of automata is an important area of theory of computation. Students feel trouble in solving automata questions. We at www.expertsmind.com offers Automata assignment help - Automata homework help and online tutoring with best qualified and experienced computer science tutor's help. We cover all topics including Tree Domains and Gorn Trees in assignment help - homework help service. Get solved problems in automata theory with step by step answers anytime from expert tutors at expertsmind.