A Traversal of a Binary Tree
Tree traversal is one of the most common operations performed on tree data structures, it is a way in which each node in the tree is visited exactly once in a systematic manner. There are many applications that essentially require traversal of binary trees. For example a binary tree could be used to represent an arithmetic expression as shown below:
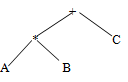
Binary tree with arithmetic expression.
The full binary tree traversal would produce a linear order for the nodes in a binary tree, there are the popular ways of binary traversal they are ;
1. Preorder traversal
2. In order traversal
3. Post order traversal
Let us examine each of these traversals in turn.
Here all the three ways are defined recursively. This helps in simply visiting the root node and traversing the left and right sub tree of a binary tree. Note that we have nothing to do with empty binary tree. So, we consider non-empty binary tree for the purpose of traversal.
1B Inorder Traversal
The inorder traversal of a non-empty binary tree is defined as follows:
1. Traverse the left sub tree in inorder (L)
2. Visit the root node (N)
3. Traverse the right subtree in inorder(R)
That is in an inorder traversal the left subtree is traversed recursively in inorder before visiting the root node. After visiting the root node, the right subtree is taken up and it is traversed recursively again in inorder. The inorder traversal of the binary tree shown below
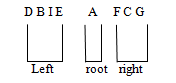
The algorithm in C for an inorder traversal is given below:
Void inorder (node *p) the name for the root
{
If (tree! = NULL)
{ inorder (p-> left);
Printf ("%d\n", p-> num)
Inorder (p-> right);
}
}
Preorder Traversal
The preorder traversal of a non-empty binary tree is defined as follows:
1. Visit the root node (N).
2. Traverse the left sub tree in preorder (L).
3. Traverse the right sub tree in preorder(R)
That is in a preorder traversal traversal the root node is visited (or processed) before traversing its left and right sub tree. The preorder notion is recursive in nature so even within the left sub tree and right sub tree the above three steps are followed. The preorder traversal of binary tree shown in Fig 8.15 is
The algorithm in c for the preorder traversal is given below:
Void preorder (node*p)
{
If (tree! = NULL)
{ printf ("%d\n", p num);
Preorder (p left);
Preorder (p right);
}
}
Postorder Traversal
The postorder traversal of non-empty binary tree is defined as follows:
1. Traverse the left sub tree in postorder (L).
2. Traverse the right sub tree in postorder (R).
3. Visit the root node (N).
That is, in a postorder traversal the left and right sub tree are recursively processed before visiting the root. The left sub tree is taken up first and is traversed in post order. Then the right sub tree is taken up and is traversed in post order. Finally the data of the root node is displayed.
The algorithm in C for post order traversal is given below;
Void post order (node *p)
{
If (tree! = NULL)
{ Post order (p left);
Post order (p right);
Printf ("%d\n", p num);
}
}
Here is the complete program to create a binary tree and traverse it inorder it in inoder , preorder and post order.
Non-Recursive traversal
The binary tree is also traversed in non-recursive way using stack.
Preorder Traversal
Algorithm
Preorder. This algorithm traverses the tree in preorders non-recursively using stack. Initially push NULL onto stack and then set p = ROOT. Then repeat the following steps input
P! = NULL
Step 1. Proceed down the left most path rooted at p processing each node N on the path and pushing each right child, p right. If any onto STACK. The traversing ends after a node N with no left child L (N) is processed.
Therefore the pointer P is updated using the assignment P = P left and the traversing stops when P Left =NULL
Step 2. Pop the element from stack and assign to p. if p = NULL then return step 1 else exit.
In order Traversal
Algorithm
In order. This algorithm traverses the tree non-recursively in Inorder using STACK Initially PUSH NULL onto stack & then set P= ROOT and the repeat the following steps until NULL is popped from stack.
Step 1. Proceed down the left most path rooted at P pushing each node N onto STACK and stopping when a node N With no left child is pushed onto stack.
Step 2. Pop and process the nodes on STACK. If NULL is popped then exit. If a node N with a right child P= right is processed set p=p right and return to step
Post order Traversal
Algorithm
Post order traversal. This algorithm traverses the tree non recursively in post order using stack. Initially push NULL onto STACK and then set p= ROOT. Then repeat the following steps until NULL is popped from STACK.
Step 1. Proceed down the left most path rooted an of path push n onto STACK and if N has a right child p right push p right onto stack.
Step 2. Pop and process positive nodes an STACK. If NILL is popped then exit if a negative node is popped i.e. if p = - N for some Node N, set p= N and return to step
Data Structure & Algorithms Assignment Help, Live Experts
Struggling with data structure problems? Data structure subject is quite tough to learn? Need quick assistance in data structure questions? ExpertsMind.com is right place for you where your search ends, We at ExpertsMind offer online data structure assignment help, data structure homework help and data structure and algorithms question's answers by best online support by qualified tutors.
ExpertsMind.com - Traversal of a Binary Tree Assignment Help, Traversal of a Binary Tree Homework Help, Traversal of a Binary Tree Assignment Tutors, Traversal of a Binary Tree Solutions, Traversal of a Binary Tree Answers, Binary Trees Assignment Tutors