Transportation Problem in Linear Programming

The transportation problem is a special case of linear programming. In its most general form, the transportation problem has a number of origins and a number of destinations. A certain quantity of commodity is produced or manufactured at each origin and it is to be transported to the destinations, each having certain requirements. The objective of the problem is to meet the destination requirements with supply from the origins so that transportation costs are minimal.

This method is applicable in situations involving the physical movement of goods from plants to warehouses, warehouses to wholesalers, wholesalers to retailers and from retailers to customers. These models can also be applied to tasks like production scheduling and inventory control. Moreover, such models reduce the computational effort involved in the simplex method and are hence preferred by many operations managers.

A transportation problem can be either balanced or unbalanced. It is said to be balanced if the quantity of goods produced is equal to the total requirement of all the warehouses. Otherwise, the problem is said to be an unbalanced one. In an unbalanced problem, a dummy warehouse is added if the production capacity is more than the requirement, and a dummy origin is added if production capacity is less than the requirement with desired quantity to make it a balanced problem.

Since the formulation of a transportation problem is a special type of linear programming, it can be formulated as a linear programming problem as shown below.

Suppose X_ij is the quantity transported from the plant P_i to a warehouse W_j, and C_ij is the unit transportation cost from P_i to W_j.

Since the objective of a transportation problem is to minimize the total transportation cost, the objective function can be given as,

Minimize, Z = ∑C_ij X_ij

Subject to the supply constraints

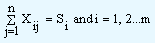
Demand constraints

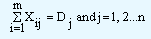
And  X_ij >= 0     for all i and j, where:

• X_ij represents the number of units shipped from origin i to destination j

• C_ij represents the cost of shipping a unit from origin i to destination j

• S_i represents the supply available at i^th origin

• D_j represents the quantity demanded at j^th destination

The general layout of the transportation problem in table form is given in table 4.7.

A transportation problem can be solved by using the following procedure:

Step 1: Define the objective function that is to be minimized.

Step 2: Develop a transportation table with rows representing the origins and columns representing the destinations.

Step 3: Determine the initial feasible solution to the problem.

Step 4: Examine whether the initial solution is feasible or not. A solution is feasible, if the number of occupied cells in the solution is (m+n-1), where 'm' is the number of origins and 'n' is the number of destinations.

Step 5: Test the solution obtained for optimality by computing the opportunity costs associated with the unoccupied cells.

Step 6: If the solution is not optimum, modify the allocation such that the transportation cost can be reduced further.            

Developing an Initial Feasible Solution

The methods used to determine an initial feasible solution are:

• North-West corner method

• Least cost method

• Vogel's approximation method

Email based Operations Management assignment help - homework help at Expertsmind

Are you searching Operations Management expert for help with Transportation Problem in Linear Programming questions? Transportation Problem in Linear Programming topic is not easier to learn without external help?  We at www.expertsmind.com offer finest service of Operations Management assignment help and Operations Management homework help. Live tutors are available for 24x7 hours helping students in their Transportation Problem in Linear Programming related problems. We provide step by step Transportation Problem in Linear Programming question's answers with 100% plagiarism free content. We prepare quality content and notes for Transportation Problem in Linear Programming topic under Operations Management theory and study material. These are avail for subscribed users and they can get advantages anytime.

Why Expertsmind for assignment help

1. Higher degree holder and experienced experts network
2. Punctuality and responsibility of work
3. Quality solution with 100% plagiarism free answers
4. Time on Delivery
5. Privacy of information and details
6. Excellence in solving Operations Management questions in excels and word format.
7. Best tutoring assistance 24x7 hours